Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата




                                                         

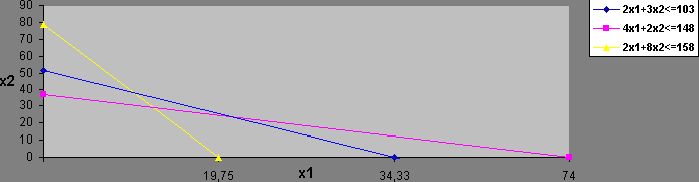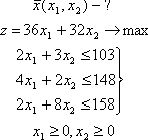
Следует при этом обратить внимание на то, что последовательное улучшение производственной программы  (x1=0, x2=0) ® (x1=37, x2=0) ® (x1=31, x2=12) на графике означает движение от одной вершины многогранника допустимых решений к другой вершине по связывающей их стороне многоугольника.

  ДВОЙСТВЕННАЯ ЗАДАЧА

Ранее мы рассмотрели конкретную линейную производственную задачу по выпуску четырех видов продукции с использованием трех видов ресурсов по заданным технологиям.

Теперь представим себе, что знакомый предприниматель П, занимающийся производством каких-то других видов продукции, но с использованием трех таких же видов ресурсов, какие имеются у нас, предлагает нам "уступить" по определенным ценам все имеющиеся у нас ресурсы и обещает платить у1 рублей за каждую единицу первого ресурса, у2 руб – второго, у3 руб – третьего. Возникает вопрос: при каких ценах у1, у2, у3 мы можем согласиться с предложением П.

Величины у1, у2, у3 принято называть расчетными, или двойственными, оценками ресурсов. Они прямо зависят от условий, в которых действует наше предприятие.

Напомним, что в нашей задаче технологическая матрица А, вектор объемов ресурсов В и вектор удельной прибыли С имели вид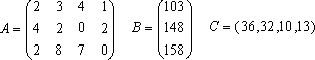 

Для производства единицы продукции первого вида мы должны затратить, как видно из матрицы А, 2 единицы ресурса первого вида, 4 единицы ресурса второго вида и 2 единицы третьего (элементы первого столбца матрицы). В ценах у1, у2, у3 наши затраты составят 2у1 + 4у2 + 2у3, т.е. столько заплатит предприниматель П за все ресурсы, идущие на производство единицы продукции первого вида. На рынке за единицу первой продукции мы получили бы прибыль 36 руб. Следовательно, мы можем согласиться с предложением П только в том случае, если он заплатит не меньше 2у1 + 4у2 + 2у3 ³ 36.

Аналогично, для трех оставшихся видов продукции:

3у1 + 2у2 + 8у3³32

4у1 +          7у3³10

 у1 + 2у2          ³13

Учтем, что за все имеющиеся у нас ресурсы нам должны заплатить   103у1 + 148у2 + 158у3 рублей. При поставленных нами условиях предприниматель П будет искать такие значения величин у1, у2, у3, чтобы эта сумма была как можно меньше. Подчеркнем, что здесь речь идет не о ценах,  по которым мы когда-то приобретали эти ресурсы, а об этих ценах, которые существенно зависят от применяемых нами технологий, объемов ресурсов и от ситуации на рынке.

Таким образом, проблема определения расчетных оценок ресурсов приводит к задаче линейного программирования: найти вектор двойственных оценок  у(у1, y2, y3) минимизирующий общую оценку всех ресурсов                       f =  103у1 + 148у2 + 158у3                      (1)

при условии, что по каждому виду продукции суммарная оценка всех ресурсов, затрачиваемых на производство единицы продукции, не меньше прибыли, получаемой от реализации единицы этой продукции

2у1 + 4у2 + 2у3 ³ 36

3у1 + 2у2 + 8у3³32                                          (2)

4у1 +          7у3³10

 у1 + 2у2          ³13

причем оценки  ресурсов не могут быть отрицательными  y10,  y20,  y30.       (3)

Решение полученной задачи легко найти с помощью второй основной теоремы    двойственности,  согласно     которой     для     оптимальных решений   (х1, х2, х3, х4)    и   (y1, y2, y3) пары двойственных задач необходимо и достаточно выполнение условий

       x 1 (2у1 + 4у2 + 2у3 - 36) = 0                          y1 (2x1 +3x2 + 4x3 + x4 - 103) = 0

       x 2 (3у1 + 2у2 + 8у3 - 32) = 0                       y2 (4x1 +2x2           + 2x4 - 148) = 0

  x 3  (4у1 +          7у3-  10) = 0                             y3 (2x1 +8x2 + 7x3              - 158) = 0         .

       x 4  (у1   + 2у2          -  13) = 0             

Ранее было найдено, что в решении исходной задачи х1>0,  x2>0.  Поэтому

Рекомендуем скачать другие рефераты по теме: реферат по английскому, докладная записка.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки