Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата

Чуть позже мы рассмотрим построение на одном рисунке графиков плотности и векторного поля, а также создание более наглядных жирных стрелок.

13.6.6. Графики в разных системах координат

В пакете plots имеется множество функций для построения графиков в различных системах координат. Объем книги не позволяет воспроизвести примеры на все виды таких графиков, ибо их многие сотни. Да это и не надо — во встроенных в справочную систему примерах можно найти все нужные сведения. Так что ограничимся лишь парой примеров применения функции tubeplot(C, options), позволяющей строить весьма наглядные фигуры в пространстве, напоминающие трубы или иные объекты, образованные фигурами вращения.

На рис. 13.32 показана одна из таких фигур. Она поразительно напоминает раковину улитки. Функциональная окраска достигнута доработкой графика с помощью панели форматирования. Смысл параметра С (в документе Conchoid) легко понять из этого примера.

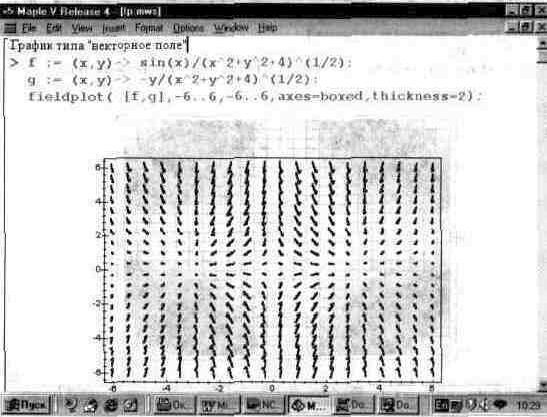
Рис. 13.31. Двумерный график типа векторного поля.

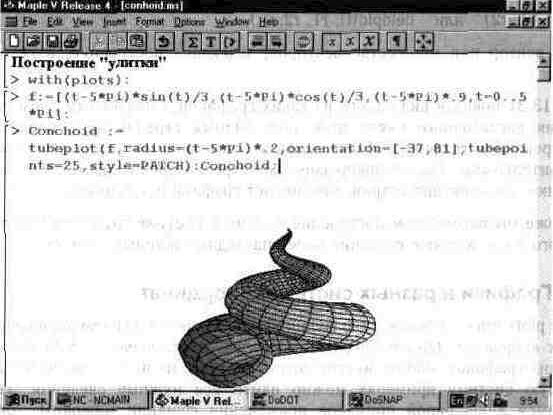
Рис. 13.32. Построение графика «улитки».

Эта функция может использоваться и для построения ряда трубчатых объектов в пространстве. При этом автоматически задается алгоритм удаления невидимых линий даже для достаточно сложных фигур. Это наглядно иллюстрирует пример

на рис. 13.33, показывающий фигуру «цепи». Не правда ли реалистичность этой фигуры поражает воображение?

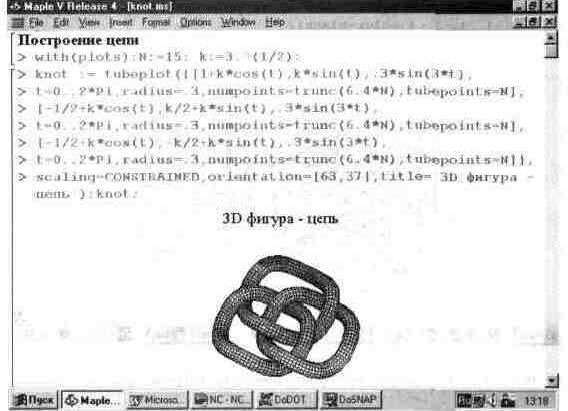
Рис. 13.33. Фигура «цепи», построенная с применением функции tubeplot.

Можно немало размышлять о том, как природа «узнала» о математических закономерностях, положенных в основу тех или иных геометрических объектов, или, возможно, о гениальности людей, сумевших найти такие закономерности для природных объектов. В наше время Maple V открывает огромные возможности для таких людей.

13.6.7. Графики типа трехмерного векторного поля

Наглядность ряда графиков можно существенно увеличить, строя их в трехмерном представлении. Например, для такого построения векторных полей можно использовать графическую функцию fieldplot3d. В отличие от функции fieldplot, она строит стрелки как бы в трехмерном пространстве (рис. 13.34).

Все сказанное об особенностях таких двумерных графиков остается справедливым и для графиков трехмерных. В частности, для получения достаточной их представительности нужно тщательно отлаживать форматы представления таких графиков.

13.6.8. Контурные трехмерные графики

В отличие от векторных графиков, контурные графики трехмерных поверхностей, наложенные на сами эти поверхности, нередко повышают восприимчивость таких поверхностей — подобно изображению линий каркаса. Для одновременного построения трехмерной поверхности и контурных линий на них служит функция contourplot3d. Пример ее применения показан на рис. 13.35.

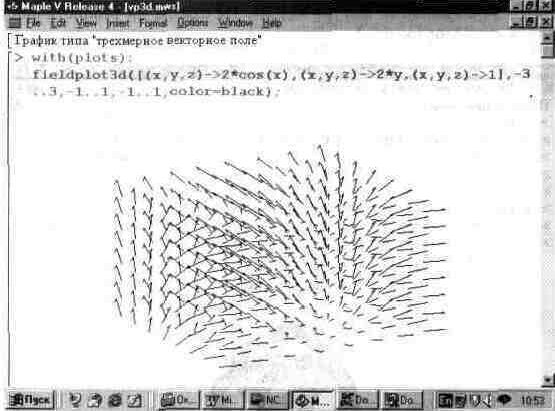
Рис. 13,34. Построение векторного поля в трехмерном пространстве.

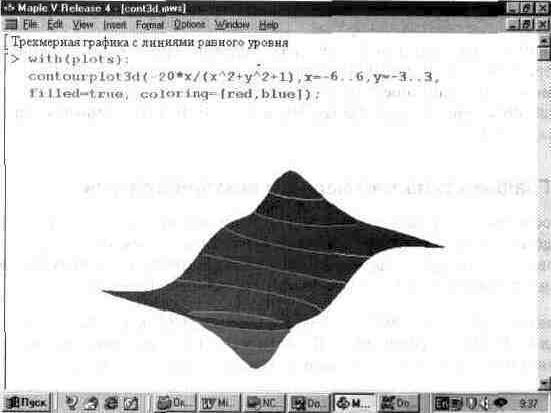
Рис. 13.35. График трехмерной поверхности с контурными линиями.

Для повышения наглядности этот график доработан с помощью панели форматирования графиков. В частности, включена функциональная окраска и подобраны углы обзора фигуры, при которых отчетливо видны впадина и пик фигуры.

13.6.9. Техника визуализации сложных пространственных фигур

Приведенные выше достаточно простые примеры дают представление о высокой степени визуализации геометрических фигур с помощью пакета plots. Здесь мы рассмотрим еще несколько примеров визуализации трехмерных фигур. Многие видели катушки индуктивности, у которых провод того или иного диаметра намотан на тороидальный магнитный сердечник. Математическая абстракция такой катушки показана на рис. 13.36.

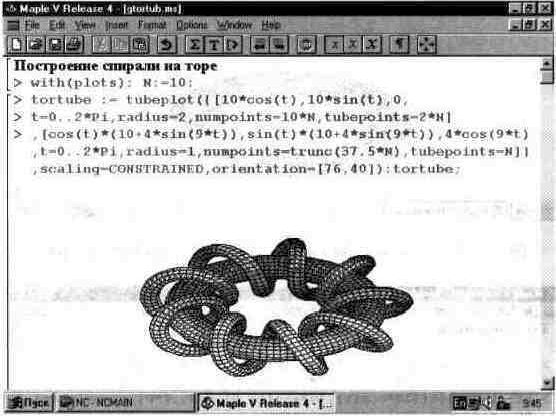
Рис. 13.36. Top с обмоткой — толстой спиралью.

В документе (рис. 13.36) для функции tubeplot использовано довольно большое число параметров-опций. Не всегда их действие очевидно. Поэтому на рис. 13.37 показано построение трех взаимно пересекающихся торов с разными типами их построения. Этот рисунок дает также наглядное представление о возможности построения нескольких графических объектов (представленных функциями р1, р2 и рЗ) с помощью функции tubeplot.

Наконец, на рис. 13.38 показано построение тора с тонкой обмоткой. Рекомендуется внимательно просмотреть запись функции tubeplot в этом примере и в примере, показанном на рис. 13.36. Можно также поэкспериментировать с опциями графика, от которых сильно зависит его представительность и наглядность.

В ряде случаев наглядно представленные фигуры можно строить с применением объединения однотипных фигур. Пример графика подобного рода представлен на рис. 13.39. Здесь готовится список графических объектов s, смещенных по вертикали. С помощью функции display они воспроизводятся на одном графике, что повышает реалистичность изображения.

Последний пример имеет еще одну важную особенность — он иллюстрирует задание графической процедуры, в теле которой используются функции пакета

Рекомендуем скачать другие рефераты по теме: евгений сочинение, шпаргалки по праву.



Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки