Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

Для обычного графического представления результатов решения дифференциальных уравнений может использоваться функция odeplot из описанного выше пакета plots. Эта функция используется в следующем виде:

odeplot(s,vars,r,o),

где s — запись (в выходной форме) дифференциального уравнения или системы дифференциальных уравнений, полученных при их численном решении функцией dsolve, vars — переменные, r — параметр, задающий пределы решения (например, а..Ь) и о — не обязательные дополнительные опции.

На рис. 13.47 представлен пример решения одного дифференциального уравнения с выводом решения у(х) с помощью функции odeplot.

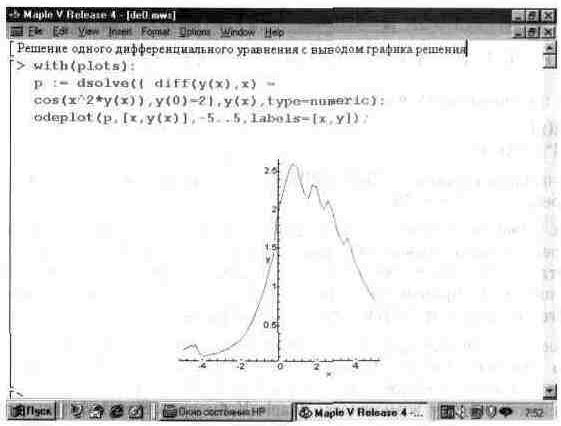
Рис. 13.47. Пример решения одного дифференциального уравнения.

В этом примере решается дифференциальное уравнение y'(x)=cos(x"2*y(x))

при у(0)=2 и х, меняющемся от -5 до 5. Левая часть уравнения записана с помощью функции вычисления производной diff. Результатом построения является график решения у(х).

На другом примере (рис. 13.48) представлено решение системы из двух нелинейных дифференциальных уравнении. Здесь с помощью функции odeplot строятся графики двух функций — у(х) и z(x).

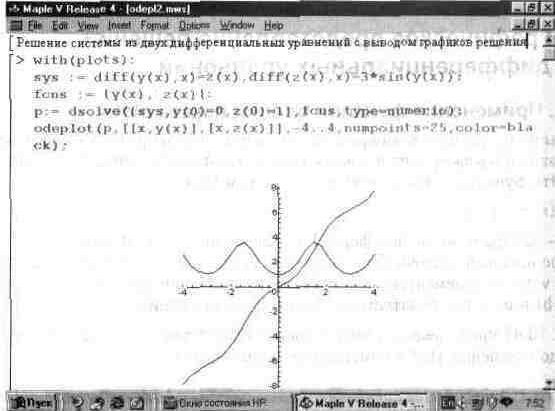
Рис. 13.48. Пример решения системы из двух дифференциальных уравнении

В этом примере решается система:

y'(x)=z(x) z'(x)=3*sin(y(x))

при начальных условиях у(0)=0, z(0)=l и х, меняющемся от -4 до 4 при числе точек решения, равном 25.

Иногда решение системы из двух дифференциальных уравнений (или одного дифференциального уравнения второго порядка) представляется в виде фазового портрета — при этом по осям графика откладываются значения у(х) и z(x) при изменении х в определенных пределах. Рис. 13.49 представляет построение фазового портрета для системы, представленной выше.

Обычное решение, как правило, более наглядно, чем фазовый портрет решения. Однако для специалистов (например, в теории колебаний) фазовый портрет порою дает больше информации, чем обычное решение. Он более трудоемок при построениях, поэтому возможность Maple V быстро строить фазовые портреты трудно переоценить.

13.8.2. Функция DEplot из пакета DEtools

Специально для решения и визуализации решений дифференциальных уравнений и систем с дифференциальными уравнениями служит инструментальный пакет DEtools. В него входит ряд функций для построения наиболее сложных и изысканных графиков решения дифференциальных уравнений. Основной из этих функций является функция DEplot. '

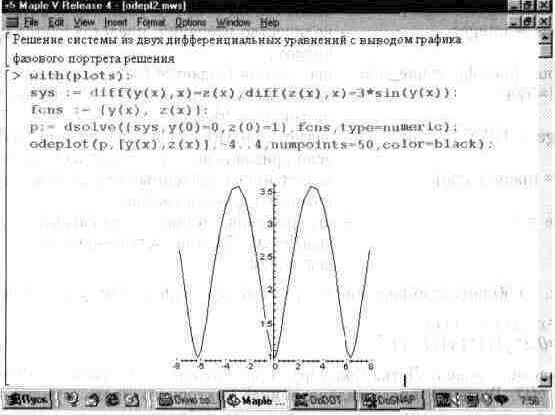
Рис. 13.49. Представление решения системы дифференциальных уравнений в виде фазового портрета.

Функция DEplot может записываться в нескольких формах:

DEplot(deqns, vars, trange, eqns) DEplot(deqns, vars, trange, inits, eqns) DEplot(deqns, vars, trange, yrange, xrange, eqns) DEplot(deqns, vars, trange, inits, xrange, yrange, eqns)

Здесь: deqns — лист (множество) с системой дифференциальных уравнении первого порядка или одиночное уравнение любого порядка, vars — зависимая переменная (лист) либо множество зависимых переменных, trange — область изменения независимой переменной t, inits — начальные условия для решения, yrange — область изменения для первой зависимой переменной, xrange — область изменения для второй зависимой переменной, eqns — опция, записываемая в виде keyword=value. Замена имен переменных другими в данном случае не допустима.

Эта функция обеспечивает численное решение дифференциальных уравнений или их систем при одной независимой переменной t и строит графики решения. Для автономных систем эти графики строятся в виде векторного поля направлений, а для неавтономных систем только в виде кривых решения. По умолчанию реализуется метод Рунге-Кутта 4-го порядка, что соответствует опции method=classi-cal[rk4]. Возможна спецификация и других методов (см. главу 10). В каталоге EXAMPLE системы Maple V R4 можно найти файл deplot.mws с многочисленными примерами применения функции DEplot.

С функцией DEplot могут использоваться следующие опции о:

arrows = type — тип стрелки векторного поля ('SMALL',

'MEDIUM', 'LARGE', 'LINE' или 'NONE');

colour, color = arrowcolour — цвет стрелок (задается 7 способами);

Рекомендуем скачать другие рефераты по теме: евгений сочинение, шпаргалки по праву.



Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки