Исследование некоторых задач в алгебрах и пространствах программ

Казиев В.М.

Рассмотрим пару алгебр (A,B): алгебру X= событий - алгоритмических процедур (программ) заданную над алфавитом X={x1,x2,...,xn} и В-трехзначную алгебру логики (0,1,2 - неопределенность). В алгебре А определим двухместные операции конъюнкции и условной дизъюнкции и одноместную операцию итерации следующим образом: конъюнкция s1&s2 событий s1, s2 состоит из всех слов вида pq, pÎ s1, qÎ s2; a - дизъюнкция a(s1+s2) совпадает с s1(s2), если условие a истинно (ложно); итерация с постусловием {s}a состоит из пустого события s0=e и всевозможных слов вида p1p2...pk т.е. 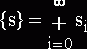, {s}a=sm, где sm - последний из степеней s, для которого условие a выполнено; итерация с предусловием a{s} определяется аналогично. В алгебре А задается событие называемое неопределенным и обозначаемое символом Æ. Элементарные события в А - события е, x1, x2,..., xn. Аксиомы алгебры А ниже рассмотрены. Все аксиомы алгебры B и правила вывода в ней сохраняются. Правила вывода, используемые в алгебре А включают правила вывода, принятые в программировании - см., например, [1]. Событие, получаемое применением конечного числа операций алгебры А над элементарными, называется регулярным.

Имеет место важная теорема Клини [2]: регулярные события и только они представимы в конечных автоматах.

Рассмотрим задачу построения алгоритма регуляризации во введенной паре алгебр (А,B). Алгоритм в укрупненных шагах состоит в следующем.

Шаг 1. Задается произвольное событие s=s0 s1 s2...sn+1, где si - событие номер i, начальное событие - s0, конечное - sn+1, остальные события - преобразователи и/или события - распознаватели.

Шаг 2. Составляется система уравнений алгебры событий А: записывается функция F события, его дерево D и дерево состояний определяющее все к путей выполнения : 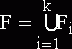, где Fi - функция ветви дерева состояний. Функция ветви дерева - композиция всех функций (событий) данной ветви; программная функция F - объединение всех функций ветвей дерева.

Шаг 3. Система уравнений с помощью подстановок и операций дизъюнкции и конъюнкции представляется в виде : X=XA+B, где X - событие, представленное заключительным состоянием sn+1, .

Шаг 4. Находим решение системы. Используется теорема [3]: если характеристический граф матрицы А (орграф соединяющий ребрами вершины i и j только тогда, когда eÎaij) не содержит ни одного цикла, то система X=XA+B имеет единственное решение X=B{A}, которое регулярно при регулярных A, B. При решении системы эффективно преобразовывать уравнения, - как и при решении линейных алгебраических уравнений, например, брать дизъюнкцию событий, изменять порядок исключения событий и др.

Шаг 5. По условиям выполнимости событий находим регулярную форму этого решения. Используются аксиомы алгебры логики В и соотношения алгебры событий А, например, следующие (AB=A&B, ab=a&b,a(A) - условие выполнимости события А, Aa - проверка условия a после события А и для этого условия верны все аксиомы алгебры В,  - отрицание условия a):

Ae=eA=A,

ea=a(e)=a,

AÆ=ÆA=Æ,

2(A+B)=Æ,

a(b(A))=b,

A(BC)=(AB)C,

b(A+B)=(a(A)+  (B)),

a(b(A+B))=(ba(A))+( (B)),

a(A+B)C=a(AC+BC),

Aa(B+C)=a(AB+AC),

a(AB)=a(A)Ba(B),

(AB)a=A(Ba),

A{B}a={BAa}A,

a({A}b)={Ab}b,

{A}a=a(e+A{A}a),

{a(A)}(B)={A}B,

Рекомендуем скачать другие рефераты по теме: собрание сочинений, пожары реферат.



1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки