Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

a{A}a{A}=a{A},

{a a{A}}=a{A},

{A}a{A}a={A}a,

{{A}aa}={A}a ,

{a(A)}={A} ,

{A}a+e=a{A},

Aa{A}=a{A}A={A}a .

Пример 1. Регуляризуем микропрограмму А деления с фиксированной запятой. Для простоты считаем, что числа неотрицательны, а операция не приводит к переполнению разрядной сетки компьютера фон - Неймановского типа, операционный автомат которого состоит из регистров R1, R2 сумматора R3 и счетчика сдвигов R4. Делимое храниться на R1, делитель - на R2, частное накапливается на R3. Введем обозначения: li - микрооперация сдвига регистра Ri влево (i=1,2,3); s-1ij - микрокоманда вычитания из содержимого регистра Rj содержимого регистра Ri; ai - условие заполненности регистра Ri; gi - условие отрицательности содержимого регистра Ri; pi - микрооперация занесения единицы в младший разряд Ri; si,j- микрокоманда добавления содержимого регистра Ri к содержимому Rj.

Выпишем систему уравнений, обозначив через xi - событие соответствующее каждому из 11 пунктов алгоритма деления (см., например, [3]):

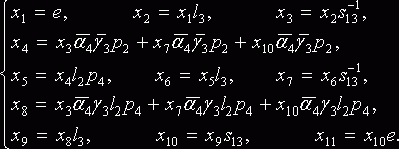
Решим эту систему. После очевидных подстановок, вводя обозначения:

x=x3+x7+x10 ,

B=el3s-113,

A=g3p2l2p4l3s-113+g3l2p4l3s-113

получим уравнение X=XA+B, решение которого будет X=B{A} и после упрощений с помощью приведенных аксиом, заключительное событие S равно

s=x11l3s-113{g3(l2p4l3s13+p2 l2p4l3s13-1)}a4

2. Рассмотрим задачу нахождения оптимальных (например, в смысле операции, длины и т.д.) структурированных программ из заданного набора базовых процедур (некоторые из них - см. в [5]), а также построения грамматик для анализа структур из программных единиц. При решении этой задачи используются аксиомы алгебры А.

Пример 2. Дана программа Р, где А,В,С - процедуры, a,b - предикаты:

P=a(BA+CA)b(Ab{A}+e)=a(B+С)Ab(Ab{A}+e)=a(B+С)Ab({A}b+e)=a(B+С)Ab{A}=a(B+C){A}b=T.

Программа Т - более оптимальна и ее правильность доказываема формально.

Доказана теорема (доказательство не приводим из-за объема).

Теорема 1. Если R,A,S Î A, a,b,gÎB, A и S - коммутативны, то:

а)AX=Aa(R+SX)ÛAX=A{S}aR, б)Ag=Aa(b+Sg)ÛAg=A{S}ab,

в)Ag=Aa(b+S )ÞAg=A{S2}ta(b+S ),t=a+Sa,

г)Ag=A{S2}tgÞAg=At(e+S2)g, g=a(b+S), t=a+Sa.

Рекомендуем скачать другие рефераты по теме: собрание сочинений, пожары реферат.



Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки