Предыдущая страница реферата | 10  11  12  13  14  15  16  17  18  19  20 | Следующая страница реферата

Решение:

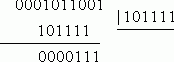
Остаток не нулевой, комбинация бракуется. Указать ошибочные разряды при трехкратных искажениях такие коды не могут.

III. Циклические коды, исправляющие две и большее количество ошибок,

Методика построения циклических кодов с  отличается от методики построения циклических кодов с  только в выборе образующего многочлена. В литературе эти коды известны как коды БЧХ (первые буквы фамилий Боуз, Чоудхури, Хоквинхем - авторов методики построения циклических кодов с ).

Построение образующего многочлена зависит, в основном, от двух параметров: от длины кодового слова п. и от числа исправляемых ошибок s. Остальные параметры, участвующие в построении образующего многочлена, в зависимости от заданных  и могут быть определены при помощи таблиц и вспомогательных соотношений, о которых будет сказано ниже.

Для исправления числа ошибок  еще не достаточно условия, чтобы между комбинациями кода минимальное кодовое расстояние . необходимо также, чтобы длина кода  удовлетворяла условию

                                                                    (79)

при этом п всегда будет нечетным числом. Величина h определяет выбор числа контрольных символов  и связана с  и s следующим соотношением:

                                                    (80)

С другой стороны, число контрольных символов определяется образующим многочленом и равно его степени. При больших значениях h длина кода п становится очень большой, что вызывает вполне определенные трудности при технической реализации кодирующих и декодирующих устройств. При этом часть информационных разрядов порой остается неиспользованной. В таких случаях для определения h удобно пользоваться выражением

                                                                 (81)

где  является одним из сомножителей, на которые разлагается число п.

Соотношения между , С и h могут быть сведены в следующую таблицу

№ п/п
10	10 11 12	15 31 63 127 255 511 1023 2047 4095	5; 3 7; 3; 3 17; 5; 3 7; 3; 7 31; 11; 3 89; 23 3; 3; 5; 7; 13

Например, при h = 10 длина кодовой комбинации может быть равна и 1023  и 341 (С = 3), и 33 (С =31), и 31 (С = 33), понятно, что п не может быть меньше  Величина С влияет на выбор порядковых номеров минимальных многочленов, так как индексы первоначально выбранных многочленов умножаются на С.

Построение образующего многочлена  производится при помощи так называемых минимальных многочленов , которые являются простыми неприводимыми многочленами (см. табл. 2, приложение 9). Образующий многочлен представляет собой произведение нечетных минимальных многочленов и является их наименьшим общим кратным (НОК). Максимальный порядок  определяет номер последнего из выбираемых табличных минимальных многочленов

                                                                           (82)

Порядок многочлена используется при определении числа сомножителей . Например, если s = 6, то . Так как для построения  используются только нечетные многочлены, то ими будут:  старший из них имеет порядок . Как видим, число сомножителей  равно 6, т. е. числу исправляемых ошибок. Таким образом, число минимальных многочленов, участвующих в построении образующего многочлена,

                                                                      (83)

а старшая степень

                                                                      (84)

( указывает колонку в таблице минимальных многочленов, из которой обычно выбирается многочлен для построения ).

Степень образующего многочлена, полученного в результате перемножения выбранных минимальных многочленов,

                                                          (85)

В общем виде

Рекомендуем скачать другие рефераты по теме: реферат федерация, сочинение капитанская.

Предыдущая страница реферата | 10  11  12  13  14  15  16  17  18  19  20 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки