Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Если y=ax,, 1 < x < p-1, где  - фиксированный элемент поля GF(p), то x=loga y над GF(p). Имея x, легко вычислить y. Для этого потребуется 2 ln(x+y) операций умножения.

Обратная задача вычисления x из y будет достаточно сложной. Если p выбрано достаточно правильно, то извлечение логарифма потребует вычислений, пропорциональных

L(p) = exp { (ln p  ln ln p)0.5 }

Для обмена информацией первый пользователь выбирает случайное число x1, равновероятное из целых 1,...,p-1. Это число он держит в секрете, а другому пользователю посылает число

y1 = ax1 mod p

Аналогично поступает и второй пользователь, генерируя x2 и вычислив y2, отправляя его первому пользователю.

В результате этого они могут вычислять  k12 = ax1x2 mod p.

Для того, чтобы вычислить k12, первый пользователь возводит y2 в степень x1. То же делает и второй пользователь. Таким образом, у обоих пользователей оказывается общий ключ k12, который можно использовать для шифрования информации обычными алгоритмами. В отличие от алгоритма RSA, данный алгоритм не позволяет шифровать собственно информацию.

Не зная x1  и x2, злоумышленник может попытаться вычислить k12, зная только перехваченные y1  и y2. Эквивалентность этой проблемы проблеме вычисления дискретного логарифма есть главный и открытый вопрос в системах с открытым ключом. Простого решения до настоящего времени не найдено. Так, если для прямого преобразования 1000-битных простых чисел требуется 2000 операций, то для обратного преобразования (вычисления логарифма в поле Галуа) - потребуется около 1030 операций.

Как видно, при всей простоте алгоритма Диффи-Хелмана, его недостатком является отсутствие гарантированной нижней оценки трудоемкости раскрытия ключа.

Кроме того, хотя описанный алгоритм позволяет обойти проблему скрытой передачи ключа, необходимость аутентификации остается. Без дополнительных средств, один из пользователей не может быть уверен, что он обменялся ключами именно с тем пользователем, который ему нужен. Опасность имитации в этом случае остается.

В качестве обобщения сказанного о распределении ключей следует сказать следующее. Задача управления ключами сводится к поиску такого протокола распределения ключей, который обеспечивал бы:

 возможность отказа от центра распределения ключей;

 взаимное подтверждение подлинности участников сеанса;

 подтверждение достоверности сеанса механизмом запроса-ответа,

 использование для этого программных или аппаратных средств;

 использование при обмене ключами минимального числа сообщений.

Иерархические схемы распределения ключей.

Рассмотрим следующую задачу.

   Пусть абоненты сети связи не равноправны между собой, а разделены на "классы безопасности" C1,C2,…,Cn. На множестве этих классов определен некоторый частичный порядок; если Cj < Ci, то говорят, что Ci доминирует Cj , т.е. имеет более высокий уровень безопасности, чем Cj . Задача состоит в том, чтобы выработать секретные ключи ki для каждого класса Ci таким образом, чтобы абонент из Ci мог вычислить kj в том и только в том, когда Ci ³ Cj.

Эта задача была решена в общем виде Эклом и Тейлором в связи с проблемой контроля доступа. В их методе каждый класс безопасности получает, кроме секретного, также и открытый ключ, который вместе с секретным ключом класса, доминирует данный, позволяет последнему вычислить секретный ключ данного класса.

Для случая, когда частичный порядок      является деревом, имеется схема Сандху [San], которая позволяет добавлять новые классы безопасности без изменения ключей существующих классов.

   Приведем описание иерархической схемы распределения ключей, предложенной Ву и Чангом для случая, когда частичный порядок   является деревом.

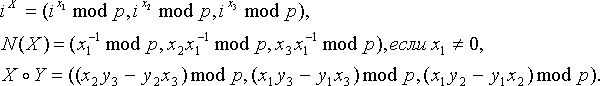Пусть p – большое простое число,  V = Zp ´ Zp ´Zp – множество всех трехмерных векторов над Zp . Если i Î Zp , X = (x1,x2,x3), Y = (y1,y2,y3) Î V, то определим следующие векторы из V:

Предположим, что каждому классу безопасности сопоставлен идентификатор

Рекомендуем скачать другие рефераты по теме: ответы 10 класс, тесты для девочек.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки