
* Алгебры и их применение
Категория реферата: Рефераты по математике
Теги реферата: изложение 8 класс, курсовые работы бесплатно
Добавил(а) на сайт: Jandiev.
Предыдущая страница реферата | 4 5 6 7 8 9 10 11 12 13 14 | Следующая страница реферата
(i) Г – векторное подпространство ![]() Н(t);
Н(t);
существует последовательность (х1, х2,…) элементов Г
таких, что для любого t![]() T элементы
хn(t) образуют последовательность H(t);
T элементы
хn(t) образуют последовательность H(t);
для любого х![]() Г функция t→||x(t)||
μ – измерима;
Г функция t→||x(t)||
μ – измерима;
пусть х – векторное поле; если для любого y![]() Г функция t→(x(t), y(t)) μ – измерима, то х
Г функция t→(x(t), y(t)) μ – измерима, то х![]() Г.
Г.
Пусть ε = ((H(t))t![]() T, Г) μ –
измеримое поле гильбертовых пространств на Т. Векторное поле х называется полем
с интегрируемым квадратом, если х
T, Г) μ –
измеримое поле гильбертовых пространств на Т. Векторное поле х называется полем
с интегрируемым квадратом, если х![]() Г и
Г и ![]() ||x(t)||2
dμ(t) < +∞.
||x(t)||2
dμ(t) < +∞.
Если х, y – с интегрируемым квадратом, то х+y и
λх (λ![]() С) – тоже и
функция t →(x(t), y(t)) интегрируема; положим
С) – тоже и
функция t →(x(t), y(t)) интегрируема; положим
(x, y) = ![]() (x(t), y(t))
dμ(t)
(x(t), y(t))
dμ(t)
Тогда векторные поля с интегрируемым квадратом
образуют гильбертово пространство Н, называемое прямым интегралом Н(t) и
обозначаемое ![]() x(t)dμ(t).
x(t)dμ(t).
Определение 2.10. Пусть ε = ((H(t))t![]() T, Г) –
измеримое поле гильбер- товых пространств на Т. Пусть для любого t
T, Г) –
измеримое поле гильбер- товых пространств на Т. Пусть для любого t![]() T определен
оператор S(t)
T определен
оператор S(t)![]() L(H(t)). Если
для любого х
L(H(t)). Если
для любого х![]() T поле t→S(t)x(t)
измеримо, то t→S(t) называется измеримым операторным полем.
T поле t→S(t)x(t)
измеримо, то t→S(t) называется измеримым операторным полем.
Пусть Т – борелевское пространство, μ -
положительная мера на Т, t→Н(t) - μ - измеримое поле гильбертовых
пространств на Т. Пусть для каждого t![]() T задано
представление π(t) *-алгебры А в Н(t): говорят, что t→π(t) есть
поле представлений А.
T задано
представление π(t) *-алгебры А в Н(t): говорят, что t→π(t) есть
поле представлений А.
Определение 2.11. Поле представлений t→π(t)
называется измеримым, если для каждого х![]() А поле
операторов t→π(t)х измеримо.
А поле
операторов t→π(t)х измеримо.
Если поле представлений t→π(t) измеримо, то
для каждого х![]() А можно
образовать непрерывный оператор π(х)=
А можно
образовать непрерывный оператор π(х)=![]() π(t) (x)
dμ(t) в гильбертовом прост- ранстве Н =
π(t) (x)
dμ(t) в гильбертовом прост- ранстве Н =![]() Н(t)
dμ(t).
Н(t)
dμ(t).
Теорема 2.9. Отображение х→π(х) есть представление А в Н.
Доказательство. Для любых х, y![]() А имеем
А имеем
π(х+y) = ![]() π(t)
(x+y) dμ(t) =
π(t)
(x+y) dμ(t) = ![]() (π(t) (x)
+ π(t) (y)) dμ(t) =
(π(t) (x)
+ π(t) (y)) dμ(t) =![]() π(t) (x
)dμ(t) +
π(t) (x
)dμ(t) +
+![]() π(t) (y)
dμ(t) = π(х) +π(y)
π(t) (y)
dμ(t) = π(х) +π(y)
Аналогично π(λх) = λπ(х), π(хy) = π(х) π(y), π(х*)=π(х)*
Определение 2.12. В предыдущих обозначениях π
называется прямым интегралом π(t) и обозначается π =![]() π(t)
dμ(t).
π(t)
dμ(t).
Определение 2.13. Операторное поле t→φ(t)I(t)![]() L(H(t)) где
I(t)-единичный оператор в H(t), называется диагональным оператором в Н=
L(H(t)) где
I(t)-единичный оператор в H(t), называется диагональным оператором в Н=![]() Н(t)dμ(t).
Н(t)dμ(t).
Пусть ε = ((H(t))t![]() T, Г) –
μ-измеримое поле гильбертовых пространств на Т, μ1 – мера на Т, эквивалентная μ (то есть каждая из мер μ1, μ абсолютно
непрерывна по другой), и ρ(t)=
T, Г) –
μ-измеримое поле гильбертовых пространств на Т, μ1 – мера на Т, эквивалентная μ (то есть каждая из мер μ1, μ абсолютно
непрерывна по другой), и ρ(t)=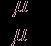 . Тогда
отображение, которое каждому х
. Тогда
отображение, которое каждому х![]() Н==
Н==![]() Н(t)dμ(t)
составляет поле t→ρ(t)-1/2х(t)Н1=
Н(t)dμ(t)
составляет поле t→ρ(t)-1/2х(t)Н1=![]() Н(t)
dμ1(t),
Н(t)
dμ1(t),
есть изометрический изоморфизм Н на Н1, называемый каноническим.
Действительно,
||![]() ρ(t)-1/2х(t)dμ1(t)||2
=
ρ(t)-1/2х(t)dμ1(t)||2
= ![]() ||х(t)||2ρ(t)-1
dμ1(t) =
||х(t)||2ρ(t)-1
dμ1(t) = ![]() ||х(t)||2dμ1(t)
= ||х(t)||2
||х(t)||2dμ1(t)
= ||х(t)||2
Теорема 2.10. Пусть Т – борелевское пространство, μ – мера на Т, t→Н(t) – измеримое поле гильбертовых пространств на Т, t→π(t) – измеримое поле представлений А в Н(t),
Н =![]() Н(t)
dμ(t) , π1==
Н(t)
dμ(t) , π1==![]() π(t
)dμ(t),
π(t
)dμ(t),
Рекомендуем скачать другие рефераты по теме: решебник 6, евгений сочинение.
Предыдущая страница реферата | 4 5 6 7 8 9 10 11 12 13 14 | Следующая страница реферата