Предыдущая страница реферата | 7  8  9  10  11  12  13  14  15  16  17 | Следующая страница реферата

Иными словами, линейное пространство L факторизируется по его линейному подмножеству, натянутому на всевозможные векторы, имеющие вид разностей между правыми и левыми частями равенств (3.6.) – (3.9.).

Затем вводится скалярное произведение в L.

(f1 f2 , g1 g2 ) = (f1 g1)(f2 g2) (3.10.)

f1, g1Н1; f2, g2 Н2,

а затем распространяется на другие элементы из факторизованного L билинейным образом.

3.2. Тензорные произведения операторов. Определим тензорное произведение ограниченных операторов.

Теорема 3.1. Пусть ,  - две последовательности гильбер- товых пространств,  - последовательность операторов АкL(Нк, Gк). Определим тензорное произведение А1 …Аn = Ак формулой

() f = () =  (3.11.)

(f ).

Утверждается, что ряд в правой части (3.11.) сходится слабо в и определяет оператор  L (, ), причем

|| || = || || (3.12.)

Доказательство. Достаточно рассмотреть случай n=2, так как в силу равенства Н1,…, Нn = (Н1,…, Нn-1)Нn общий случай получается по индукции.

Пусть - некоторый ортонормированный базис в Gк (к = 1, 2) и пусть g =  G1 G2. В качестве f возьмем вектор из Н1 Н2 с конечным числом отличных от нуля координат fα.

Зафиксируем α2, β1  Z+ и обозначим через f(α2) Н1 вектор f(α2) = 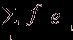 и через g(β1)G2 – вектор g(β1) =. Получим

= =

= ≤ =

= ≤ =

=

Из этого неравенства следует слабая сходимость в G1G2 ряда  уже при произвольном c Н1Н2 и оценка его нормы в G1G2 сверху через ||A1|| ||A2|| ||f||. Таким образом, оператор A1 A2: Н1 Н2 →G1G2 определен посредством (3.11.) корректно, ограничен и его норма не превосходит ||A1|| ||A2||.

Из (3.5.) и (3.11.) следует

||(A1 A2) (f1 f2)|| = ||A1 f1|| ||A2 f2|| (fк Нк , к = 1, 2)

Подбирая должным образом орты f1, f2 последнее произведение можно сделать сколь угодно близким к ||A1|| ||A2||, поэтому неравенство ||(A1 A2)|| ≤ ||A1|| ||A2|| не может выполняться, то есть (3.12.) при n=2 доказано.

Из (3.11.) получаем для Ак L(Hк, Gк), Вк L(Hк, Gк) (к = 1,…, n) соотношения

(Вк) (Ак) = (Вк Ак) (3.13.)

(Ак)* = Ак* (3.14)

Рекомендуем скачать другие рефераты по теме: решебник 6, евгений сочинение.



Предыдущая страница реферата | 7  8  9  10  11  12  13  14  15  16  17 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки