Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Пусть задана на плоскости линия уравнением (1).

Параллельный перенос:

Параллельно перенесем систему XOY на вектор OO’ т.о. что бы в системе X’O’Y’ коэфф. при x’ и y’ преобразованного уравнения кривой оказались равными нулю. После этого:

a11x’2+2a12x’y’+a22y’2+a’33=0 (2)

точка О’ находится из условия: a13’=0 и a23’=0.

Получается система a11x0+a12y0+a13=0 и a12x0+a22y0+a23=0

Покажем, что новое начало координат (если система разрешима) является центром симметрии кривой: f(x’;y’)=0, f(-x’;-y’)= f(x’;y’)

Но точка О’ существует если знаменатели у x0 и y0 отличны от нуля.

Точка O’ – единственная точка.

Центр симметрии кривой существует если I2¹ 0 т.е. центр симметрии имеют линии элиптического и гиперболического типа

Поворот:

Пусть система XOY повернута на угол u. В новой системе координат уравнение не содержит члена с x’y’ т.е. мы делаем коэфф. а12=0. a12’= -0,5(a11-a22)sin2u+a12cos2u=0 (разделим на sin2u), получим:

, после такого преобразования уравнение принимает вид

a11’x’2+a22’y’2+2a13’x’+2a23’y’+a33’=0 (3)

ТЕОРЕМА О ЛИНИЯХ ЭЛИПТИЧЕСКОГО ТИПА.

Теорема: Пусть задана линия элиптического типа т.е. I2>0 и пусть I1>0 следовательно уравнение (1) определяет: 1. I3<0 – эллипс; 2. I3=0 – точка; 3. I3>0 – ур-е (1) не определяет. Если I3=0 говорят, что эллипс вырождается в точку. Если I3>0 говорят, что задается мнимый эллипс. Пусть после ПП и поворота ур-е (1) принимает вид (*).

Доказательство:

1. пусть I2>0, I1>0, I3<0, тогда

а11’’x’’2+a22’’ y’’2= -I3/I2

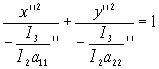
I2=a11’’a22’’ > 0

I1= a11’’+a22’’ > 0

a11’’ > 0; a22’’ > 0

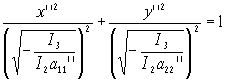
Рекомендуем скачать другие рефераты по теме: конспект, оформление доклада титульный лист.



Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки