Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Напомним, что выпуклой функцией f действительной переменной х на интервале (а,b) называется такая функция, для которой выполняется неравенство

f(a1 х1 + a2 х2) £ a1 f(х1) + a2 f(х2),

где х1 и х2 – любые две точки из интервала (а,b); a1, a2 ³ 0, причём a1 + a2 = 1.

Если для a1 ¹ 0, a2 ¹ 0 всегда имеет место строгое неравенство

f(a1 х1 + a2 х2)

то функция f называется строго выпуклой на (а;b). Геометрически выпуклая функция изображает дугу, график которой расположен ниже стягивающей её хорды (см. рис.)

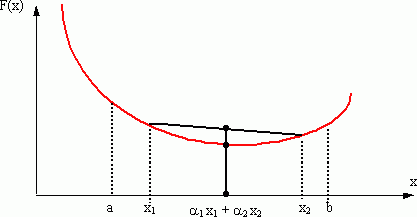
Напомним, также, что непрерывная и строго выпуклая функция f на замкнутом интервале принимает минимальное значение только в одной точке интервала.

Для нахождения решения выпуклой игры можно воспользоваться следующей теоремой.

Теорема 4. Пусть М(х, y) – непрерывная функция выигрышей игрока 1, на единичном квадрате и строго выпуклая по y для любого х. Тогда имеется единственная оптимальная чистая стратегия y = yo Î[0;1] для игрока 2, цена игры определяется по формуле

V = M(x, y),          

значение yo определяется как решение следующего уравнения

M(x, yo) = V.            

Замечание. Если в теореме 4 не предполагать строгую выпуклость функции М(х, y) по y, а просто выпуклость, то теорема остаётся в силе с тем отличием, что у игрока 2 оптимальная чистая стратегия не будет единственной.

Замечание. Выпуклые игры называют часто выпукло-вогнутыми, т.к. игра в них имеет седлообразное ядро, а так как ядро седлообразное, то игра имеет седловую точку в чистых стратегиях.

Таким образом, если М(х, y) непрерывна и выпукла по y, то цена игры определяется по формуле (1), и игрок 2 имеет оптимальную чистую стратегию, определяемую из уравнения (2).

Аналогично и для игрока 1: если функция выигрышей М(х, y) непрерывна по обоим аргументам и строго вогнута по х при любом y, то в этом случае игрок 1 имеет единственную оптимальную стратегию.

Цена игры определяется по формуле

V = M(x,y),          

а чистая оптимальная стратегия хo игрока 1 определяется из уравнения

M(xo, y) = V.            

Пример. Пусть на квадрате [0;1] задана функция

М(х, y) = .          

Так как

 для x Î[0; 1], y Î(0;1),

Рекомендуем скачать другие рефераты по теме: сочинение рассуждение, шпаргалки по математике.

Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки