Бесконечные антагонистические игры
Категория реферата: Рефераты по математике
Теги реферата: курсовая работа по менеджменту, деловое общение реферат
Добавил(а) на сайт: Boris.
Предыдущая страница реферата | 1 2 3 4 5 6 7 | Следующая страница реферата
то М(х, y) строго вогнута по х для любого y Î(0;1). Следовательно, цена игры находится по формуле (3)
V = 
.
Отметим, что при 0 £ х £
справедливо равенство
= 
а при 0,5 < х £ 1
= 
Поэтому
V = max [
; 
] =
= max [
; 
] =
= max [
;
] = 
.
При этом значение х получается равным хo = 
. Это же значение получается из решения уравнения
= 
,
т.к. минимум достигается при y = 0, и это уравнение превращается в следующее
= 
,
откуда следует, что х = 
.
Заметим, что если в функции выигрышей (5) поменять местами х и y, то она не изменится, а следовательно, эта функция выпукла и по y при всех х Î[0;1]. Поэтому к ней применима та же теория, т.е. у игрока 2 существует оптимальная чистая стратегия yo, определяемая из уравнения (4)
= 
Очевидно, максимум по х достигается при х
= 
, и последнее уравнение примет вид
= 
.
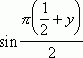Решением последнего уравнения будет yo = 0. Следовательно, игрок 2 имеет оптимальную чистую стратегию yo = 0.
Замечание. В приведённом выше примере мы могли определить оптимальную стратегию игрока 1, а игрока 2 - только случайно, в силу “удачного” вида М(х, y).
Рассмотрим теперь метод определения
оптимальных стратегий того игрока, для которого функция выигрышей не
обязательно выпукла. Пусть непрерывная функция М(х, y), заданная на единичном
квадрате, выпукла по y. Нас будет интересовать вопрос нахождения оптимальных стратегий 1
игрока. Предположим также, что для х Î[0; 1], y Î[0; 1] существует частная производная
функции М(х, y) по y, причём в точках y = 0 и y = 1 
(х, y) = 
понимается как правая
и левая производная соответственно. Обозначим через yo одну из оптимальных чистых стратегий
игрока 2 (эта стратегия существует в соответствии с теоремой 4).
Согласно теореме 2 чистые стратегии х игрока 1 могут входить в его оптимальную стратегию с положительной вероятностью, если для них выполняется равенство
М(х, yo) = V.
Такие чистые стратегии х называются существенными.
Рекомендуем скачать другие рефераты по теме: сочинение рассуждение, шпаргалки по математике.
Предыдущая страница реферата | 1 2 3 4 5 6 7 | Следующая страница реферата