Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

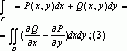
D    P(x,y), Q(x,y) ,

Вычисление площадей через крив интеграл

Применим ф. Грина, т.е. выразим его через криволинейный интеграл по границе области.

1. Q = x  P = 0

2. Q = 0   P = -y

Суммируем  1 и 2 :     

Пример: Вычислить площадь эллипса

.

Сделаем замену переменных              0 £ t £ 2p

Вопрос №6 

Неприрывную кривую назыв. простой кривой (жордановой), если она не имеет точек самопересечения.

Областью называется всякое открытое связаное мн-во, т.е. такое мн-во всякая точка кот. явл. внутренней и любые две точки этого мн-ва можно соединить непрерывной кривой все точки кот. принадлежат данному мн-ву.

Область называется односвязной областью, если внутренность всякой замкнутой кривой содержит только точки данного мн-ва. 

Теорема 1. Пусть Д  ограниченная односвязная область пл-ти x и y, тогда для того чтобы криволинейный интеграл

был равен нулю по любой замкнутой кривой ГÌД, (где P(x,y)  и Q(x,y) непрерыв. И имеет непрерыв. Частные производ.  и  ) необходимо и достаточно чтобы вып. Такое равенство

=          (2)

f(x,y)eД.

Док-во:  Пусть во всей области Д вып. Равенство (2) и Г произвольная простая замкнутая кривая принадлеж. области Д. Обознач. Через обл. Д1 кот. огранич. Эта кривая Г. Применим к этой области формулу Грина:

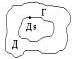
Рекомендуем скачать другие рефераты по теме: шпаргалки для студентов, титульный дипломной работы.



Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки