Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

= (2)

 

2.2. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЗВЕНА

Решим уравнение (2) относительно выходной величины y(t):

y(t)==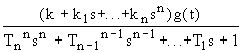

==

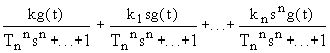=W1(s)+W2(s)+...+Wn(s)

Здесь W1(s),W2(s),...,Wn(s) - передаточные функции.

При записи уравнений с изображениями выходной и входной величин по Лапласу передаточные функции сливаются в одну.

2.3. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ЗВЕНА

Динамические свойства звена могут быть определены по его переходной функции и функции веса.

Переходная функция h(t) представляет собой переходный процесс на выходе из звена, возникающий при подаче на его вход единичного ступенчатого воздействия - скачкообразного воздействия со скачком, равной единице.

Функция веса w(t) представляет собой реакцию на единичную импульсную функцию. Она может быть получена дифференцированием по времени переходной функции:

w(t)=

2.4.ЧАСТОТНАЯ ПЕРЕДАТОЧНАЯ ФУНКЦИЯ И ЧАСТОТНЫЕ

ХАРАКТЕРИСТИКИ

Важнейшей характкристикой динамического звена является его частотная передаточная функция. Ее можно получить с помощью передаточной фкнкции, заменив линейный оператор s на комплексный jw .

Так как передаточная функция есть отношение изображения по Лапласу выходной величины к входной, то при переходе от изображения Лапласа к изображению Фурье, мы получим, что частотная передаточная функция является изображением Фурье функции веса, то есть имеет место интегральное преобразование

Рекомендуем скачать другие рефераты по теме: первый снег сочинение, реферати українською.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки