Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

 (2)

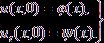 (3)

Преобразуем это уравнение к каноническому виду, содержащему смешанную производную. Уравнение характеристик

распадается на два уравнения:

, ,

интегралами которых являются прямые

, .

Вводя новые переменные

, ,

уравнение колебания струны преобразуем к виду:

. (4)

Найдем общий интеграл последнего уравнения. Очевидно, для всякого решения уравнения (4)

,

где  - некоторая функция только переменного . Интегрируя это равенство по  при фиксированном , получим

, (5)

где  и  являются функциями только переменных  и .Обратно, каковы бы ни были дважды дифференцируемые функции  и , функция , определяемая формулой (5), представляет собой решение уравнения (4). Так как всякое решение уравнения (4)может быть представлено в виде (5) при соответствующем выборе  и , то формула (5) является общим интегралом этого уравнения. Следовательно, функция

 (6)

является общим интегралом уравнения (2).

Допустим, что решение рассматриваемой задачи существует; тогда оно дается формулой (6). Определим функции  и  таким образом, чтобы удовлетворялись начальные условия:

 (7)

. (8)

Интегрируя второе равенство, получим:

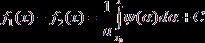
где  и C – постоянные. Из равенства

Рекомендуем скачать другие рефераты по теме: фонды реферат, соціологія шпори.



Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки