Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

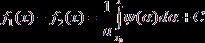
находим:

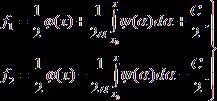 (9)

Таким образом, мы определили функции  и  через заданные функции  и , причем равенства (9) должны иметь место для любого значения аргумента. Подставляя в (6) найденные значения  и , получим:

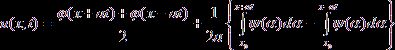
или

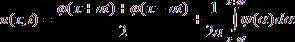, (10)

Формулу (10), называемую формулой Даламбера, мы получили, предполагая существование решения поставленной задачи. Эта формула доказывает единственность решения. В самом деле, если бы существовало второе решение задачи (2) – (3), то оно представлялось бы формулой (10) и совпадало бы с первым решением.

Нетрудно проверить, что формула (10) удовлетворяет (в предположении двукратной дифференцируемости функции  и однократной дифференцируемости функции ) уравнению и начальным условиям. Таким образом, изложенный метод доказывает как единственность, так и существование решения поставленной задачи.

2.2.2.Физический интерпретация.

Функция , определяемая формулой (10), представляет собой процесс распространения начального отклонения и начальной скорости. Если фиксировать , то функция  дает профиль струны в момент , фиксируя , получим функцию , дающую процесс движения точки . Предположим, что наблюдатель, находившийся в точке x=0 в момент t=0, движется со скоростью a в положительном направлении. Введем систему координат, связанную с наблюдателем, полагая , . В этой подвижной системе координат функция  будет определятся формулой  и наблюдатель все время будет видеть тот же профиль, что и в начальный момент. Следовательно, функция  представляет неизменный профиль f(x), перемещающийся вправо (в положительном направлении оси x) со скоростью a (распространяющуюся или бегущую волну). Функция f(x+at) представляет, очевидно, волну, распространяющуюся налево (в отрицательном направлении оси x) со скоростью a. Таким образом, общее решение (10) задачи Коши для бесконечной струны есть суперпозиция двух волн , одна из которых распространяется направо со скоростью a, а вторая – налево с той же скоростью. При этом

,

где .

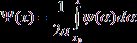Для выяснения характера решения (10) удобно пользоваться плоскостью состояний (x,t) или «фазовой плоскостью». Прямые x-at=const и x+at=const являются характеристиками уравнения (2). Функция  вдоль характеристики x-at=const сохраняет постоянное значение, функция  постоянна вдоль характеристики x+at=const.

Предположим, что f(x) отлична от нуля только в интервале  и равна нулю вне этого интервала. Проведем характеристики  и  через точки  и ; они разбивают полуплоскость (x,t>0) на три области I, II, и III (рис. 3, а).

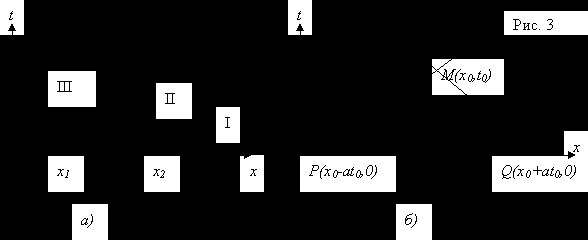
Функция  отлична от нуля только в области II, где  и характеристики  и  представляют передний и задний фронты распространяющейся направо волны.

Рассмотрим теперь некоторую фиксированную точку  и приведем из нее обе характеристики  и , которые пересекут ось x в точках , t=0 и , t=0. Значение функции  в точке  равно , т. е. определяется значениями функций и  в точках  и , являющихся вершинами треугольника MPQ (рис. 3, б), образованного двумя характеристиками и осью x. Этот треугольник называется характеристическим треугольником точки . Из формулы (10) видно, что отклонение  точки струны в момент  зависит только от значений начального отклонения в вершинах P(x0-at0,0) и Q(x0+at0,0) характеристического треугольника MPQ и от значений начальной скорости на стороне PQ. Это становится особенно ясным, если формулу (10) записать в виде

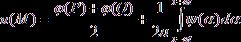 (11)

Начальные данные, заданные вне PQ, не оказывают влияния на значения  в точке . Если начальные условия заданы не на всей бесконечной прямой, а на отрезке , то они однозначно определяют решение внутри характеристического треугольника, основанием которого является отрезок .

2.2.3. Пример.

Решение (10) можно представить в виде суммы , где

 (12)

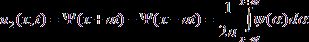. (13)

Рекомендуем скачать другие рефераты по теме: фонды реферат, соціологія шпори.



Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки