Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Пример 2. Возьмем дифференциальное уранение

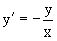или ,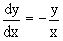

геометрическая иллюстрация решений которого рассматривается в параграфе 2.

Данное уравнение является с разделяющимися переменными> Разнося переменные в разные стороны, записываем уравнение в виде

.

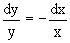Интегрирование левой и правой частей уравнения, дает общее решение вида 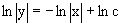, где постоянная взята в виде lnc,c>0. Далее несложно преобразовать данное уравнение к виду

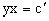или 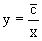, где постоянная уже не имеет ограничений на знак.

Как видно получилось семейство гипербол.

Пусть из данного семейства интегральных кривых (гипербол) необходимо выделить кривую (решение) проходящую через точку M(1,1), т.е. выделить решение, удовлетворяющее начальному условию y(1)=1. Для этого в общее решение уравнения подставим значения x=1, y=1, и найдем, отвечающее искомой кривой, значение постоянной 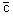. Очевидно, это значение равно 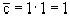. Следовательно, искомое частное решение определяется уравнением

Yx=1 или .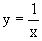

Пример 3. Рассмотрим уравнение , приведенное в параграфе 3. Разрешая его относительно y/, получаем два уравнения y/=1 и y/=-1 ил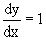и и .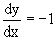

Оба являются с разделяющимися переменными и приводятся к виду dy=dx и dx=-dx. Интегрирование левых и правых частей уравнений дает следующие их общие решения y=x+c и y=-x+c.

Пример 4. Следующим уравнением возьмем уарвнение 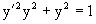из примера в параграфе 4.

Разрешая его относительно y/ получаем

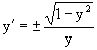или .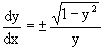

Разделяя переменные имеем

.

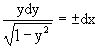Найдем интегралы от левой и правой частей уравнения:

.

.

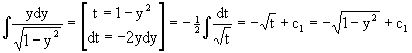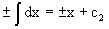Приравнивая интегралы и заменяя две постоянных на одну получаем следующий вид общего решения уравнения

.

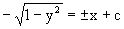Возводя в квадрат обе части данного уравнения, получаем окончательный вид общего решения

(x-c)2+y2=1.

Пример 5. Решить дифференциальное уравнение ,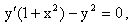

Рекомендуем скачать другие рефераты по теме: собственность реферат, шпаргалки бесплатно скачать.



Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки