Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

Потенциируя последнее выражение, общее решение получает вид 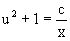, где c – произвольная постоянная.

Заменяя u=y/x, получаем общий интеграл исходного дифференциального уравнения 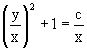или y2+x2=cx,

Последнее выражение приводится к виду

.

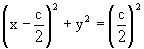Таким образом, семейством интегральных кривых исходного уравнения является семейство окружностей с центрами в точках 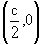, лежащих на оси x, и радиусами 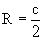. Очевидно, все эти окружности касаются оси y в точке начала координат. На рис. 6 изображено семейство этих окружностей.

Пример 2. Требуется найти частное решение уравнения ,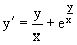

Удовлетворяющих начальному условию y(1)=0.

Нетрудно видеть (убедиться), что справа стоит однородная функция нулевой степени. Итак, исходное дифференциальное уравнение является однородным. Выполняя замену y=ux, приводим его к виду

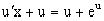или .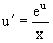

Разделяем переменные, получаем

.

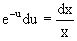Интегрируя обе части этого уравнения, получаем общее решение вспомогательного дифференциального уравнения

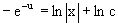или .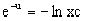

Подставим в него 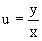и получим 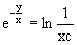. Логарифмируя обе части этого уравнения получаем 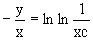и далее .

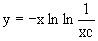Последнее соотношение дает общее решение исходного дифференциального уравнения. Чтобы найти частное решение, воспользуемся начальными условиями x=1,y=0. Подставим их в общее решение 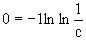, отсюда 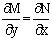и .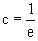

Таким образом, искомое частное решение имеет вид .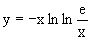

5. Линейное дифференциальное уравнение первого порядка.

Определение. Линейным дифференциальным уравнением первого порядка называется уравнение вида y/+g(x)y=h(x).

Такое название ему дано в связи с тем, что относительно переменных y и y/ его можно рассматривать как линейное.

Если 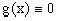, то уравнение принимает простой вид y/=h(x), и сводится к нахождению неопределенного интеграла 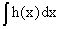. Его общее решение тогда имеет вид .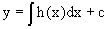

Если 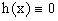, то уравнение называется однородным линейным. Оно приобретает вид 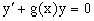, и, как нетрудно видеть, сводится к решению уравнения с разделяющимися переменными 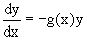и далее .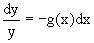

Его общее решение имеет вид 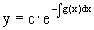, где 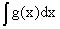- некоторая первообразная для функции g(x).

Предположим теперь, что 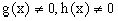, функции g(x) и h(x) являются непрерывными. Пусть y=f(x,c) – искомое общее решение линейного дифференциального уравнения.

Представим исходное уравнение в виде

,

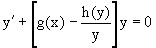и подставим в выражение, стоящее в квадратных скобках, 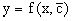, т.е. как бы полагая в общем решении 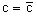. Тогда вышеприведенное уравнение примет вид

Рекомендуем скачать другие рефераты по теме: собственность реферат, шпаргалки бесплатно скачать.



Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки