Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

………………… = (xij), (i = 1,2, …, m; j = 1,2, …, n).

xm1 xm2 … xmn

Необходимо проверить существенность влияния партий изделий на их качество.

Если полагать, что элементы строк матрицы наблюдений – это численные значения случайных величин Х1,Х2,...,Хm, выражающих качество изделий и имеющих нормальный закон распределения с математическими ожиданиями соответственно a1,а2,...,аm и одинаковыми дисперсиями σ2, то данная задача сводится к проверке нулевой гипотезы Н0: a1=a2 =...= аm, осуществляемой в дисперсионном анализе.

Усреднение по какому-либо индексу обозначено звездочкой (или точкой) вместо индекса, тогда средний показатель качества изделий i-й партии, или групповая средняя для i-го уровня фактора, примет вид:

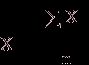, (4)

где i* – среднее значение по столбцам;

ij – элемент матрицы наблюдений;

n – объем выборки.

А общая средняя:

. (5)

Сумма квадратов отклонений наблюдений хij от общей средней ** выглядит так:

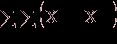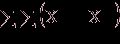2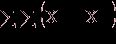=2+2+

+2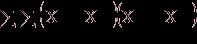2. (6)

или

Q = Q1 + Q2 + Q3.

Последнее слагаемое равно нулю

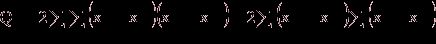=0. (7)

так как сумма отклонений значений переменной от ее средней равна нулю, т.е.

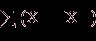2=0.

Первое слагаемое можно записать в виде:

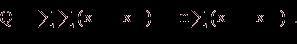
В результате получается тождество:

Q = Q1 + Q2, (8)

где 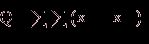- общая, или полная, сумма квадратов отклонений;

Рекомендуем скачать другие рефераты по теме: лечение шпоры, шпаргалки по экономическому.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки