Две замечательные теоремы планиметрии
Категория реферата: Рефераты по математике
Теги реферата: контрольные 7 класс, бюджет реферат
Добавил(а) на сайт: Канаев.
Предыдущая страница реферата | 1 2 3 4 5
L Q С
 |
А Д К Р
рисунок 4
прямую
LQ(P). Запишем теорему Менелая: 
Напомним, что 
РА+РC=РВ+ РD =180°.
Выразим отрезки АL и LD через перпендикуляр
KL: АL=KLЧctgРD. Отсюда 
Теперь выразим отрезки ВР и РА через МР: BP=MPЧctgРA (из D AMP),
BP=MPЧctgРMBP=MPЧctg(180°-РB)=MPЧctgРD (из D MBP).
Отсюда
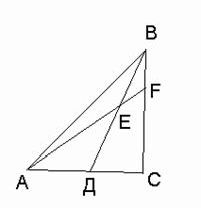
рисунок 5
Подставив найденные отношения в полученную
выше формулу имеем: 
откуда
что и требовалось доказать.
(Авторское решение построено на рассмотрении групп подобных треугольников).
В заключение вниманию читателей представляется задача, предложенная в этом году на краевой олимпиаде.
4. На стороне ВС треугольника АВС выбрана точка F. Оказалось, что отрезок АF пересекает медиану ВD в точке Е так, что АЕ=ВС. Докажите, что ВF=FЕ.
Решение: запишем теорему Менелая для треугольника САF и прямой DЕ(В):
т.к. СD=DА и АЕ=ВС, то получаем: FВ:ЕF=1 или FВ=ЕF. Что и требовалось доказать.
Скачали данный реферат: Крючков, Паллидия, Ramazanov, Dvojnev, Ткачёв, Яшкин.
Последние просмотренные рефераты на тему: бесплатный решебник, здоровье реферат, бесплатные рефераты, реферат скачать управление.
Предыдущая страница реферата | 1 2 3 4 5