
Дзета-функция Римана
Категория реферата: Рефераты по математике
Теги реферата: bestreferat, сочинения по русскому языку
Добавил(а) на сайт: Петронилла.
Предыдущая страница реферата | 1 2 3 4 5 | Следующая страница реферата
Из
(4) следует, что 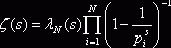 , где
, где ![]() N, а
N, а ![]() при
при ![]() . Возьмём логарифм от обеих частей равенства, тогда
. Возьмём логарифм от обеих частей равенства, тогда ![]()
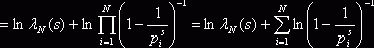 . Натуральные логарифмы под знаком суммы разлагаются в ряд:
. Натуральные логарифмы под знаком суммы разлагаются в ряд: 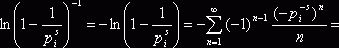
![]() . Подставив полученные разложения в равенство и устремив N к бесконечности, имеем
. Подставив полученные разложения в равенство и устремив N к бесконечности, имеем 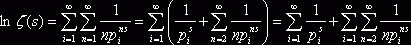 . Остаётся доказать ограниченность последнего слагаемого. Ясно, что
. Остаётся доказать ограниченность последнего слагаемого. Ясно, что ![]() . Последнее равенство справедливо, так как
. Последнее равенство справедливо, так как ![]()
![]() . Далее, очевидно,
. Далее, очевидно, ![]() , что и завершает доказательство.
, что и завершает доказательство.
На этом закончим изложение свойств дзета-функции Римана для действительного аргумента, так как наибольший теоретический и прикладной интерес представляет случай изложенный во второй главе.
Глава 2.
Все результаты первой главы, касающиеся дзета-функции Римана, были получены в предположении, что её аргумент s – действительное число. Однако, самые выдающиеся исследования и многочисленные важные приложения стали возможны лишь после включения в область определения функции комплексных чисел. Впервые рассмотрел дзета-функцию как функцию мнимого аргумента немецкий математик Бернгард Риман, глубоко изучивший её свойства и широко применявший её в теории чисел. В честь него функция получила своё название.
Для комплексной дзета-функции остаётся в силе определение, данное в главе 1, с тем лишь изменением, что теперь там будет ![]() C. Возникает необходимость найти новую
область определения. С этой целью докажем следующее утверждение: в
полуплоскости
C. Возникает необходимость найти новую
область определения. С этой целью докажем следующее утверждение: в
полуплоскости ![]() (
(![]() действительная часть числа x)
ряд
действительная часть числа x)
ряд
![]() (1) сходится абсолютно.
(1) сходится абсолютно.
Пусть ![]() . Подсчитаем абсолютные величины членов ряда (1),
. Подсчитаем абсолютные величины членов ряда (1), ![]() . Первый множитель содержит только вещественные числа и
. Первый множитель содержит только вещественные числа и ![]() , так как
, так как ![]() . Ко второму же множителю применим знаменитую формулу Эйлера, получим
. Ко второму же множителю применим знаменитую формулу Эйлера, получим ![]()
![]() . Значит,
. Значит, ![]() . Ввиду сходимости ряда
. Ввиду сходимости ряда ![]() при α>1, имеем
абсолютную сходимость ряда (1).
при α>1, имеем
абсолютную сходимость ряда (1).
На своей области определения дзета-функция аналитична.
Действительно, при всяком q>0 и
фиксированном α>1+q, числовой ряд ![]() мажорирует ряд из
абсолютных величин
мажорирует ряд из
абсолютных величин ![]() , где
, где ![]() , откуда, по теореме Вейерштрасса, следует равномерная
сходимость ряда в полуплоскости
, откуда, по теореме Вейерштрасса, следует равномерная
сходимость ряда в полуплоскости ![]() . Сумма же равномерно сходящегося ряда из аналитических
функций сама является аналитической функцией.
. Сумма же равномерно сходящегося ряда из аналитических
функций сама является аналитической функцией.
Нетрудно показать, что все полученные для дзета-функции формулы без изменений переносятся на случай комплексного аргумента. Доказательства претерпевают незначительные преобразования, связанные с переходом к абсолютным величинам.
В связи с этим замечанием становится возможным использовать
разложение дзета-функции в произведение 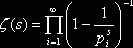 , где s теперь любое комплексное число, такое, что
, где s теперь любое комплексное число, такое, что ![]() . Применим его к доказательству отсутствия у функции
. Применим его к доказательству отсутствия у функции ![]() корней.
корней.
Оценим величину ![]() , используя свойство модуля
, используя свойство модуля ![]() :
: 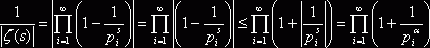 , где как обычно
, где как обычно ![]() . Так как
. Так как 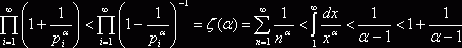 , то
, то ![]() , а
, а ![]() , следовательно, дзета-функция в нуль не обращается.
, следовательно, дзета-функция в нуль не обращается.
Вопрос о нулях дзета-функции, а также другие прикладные
вопросы получают новые широкие возможности для исследования, если
распространить её на всю комплексную плоскость. Поэтому, сейчас мы одним из
многих возможных способов найдём аналитическое продолжение дзета-функции и
выведем её функциональное уравнение, характеризующее и однозначно определяющее ![]() .
.
Для этого нам понадобится формула
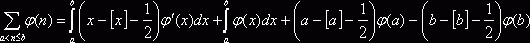 (2), которая
выводится следующим образом. Используя свойства интегралов можно записать
(2), которая
выводится следующим образом. Используя свойства интегралов можно записать 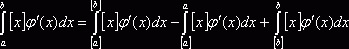 . Для любого d при
. Для любого d при ![]()
![]() , значит
, значит 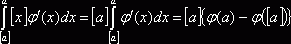 и
и 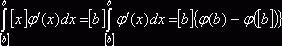 , а
, а 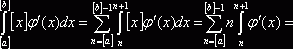 .
. 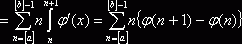 . Следовательно,
. Следовательно, 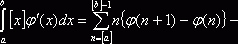
![]()
![]()
![]()
![]() . Интеграл
. Интеграл 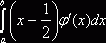 можно найти
интегрированием по частям, принимая
можно найти
интегрированием по частям, принимая ![]() ,
, ![]() ; тогда
; тогда ![]() , а
, а ![]() . В результате
. В результате 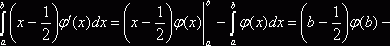
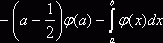 . Вычтем из этого интеграла предыдущий и получим
. Вычтем из этого интеграла предыдущий и получим 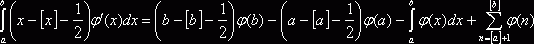 , отсюда легко следует равенство (2).
, отсюда легко следует равенство (2).
Теперь положим в (2) ![]() ,
, ![]() , a и b
– целые положительные числа. Тогда
, a и b
– целые положительные числа. Тогда 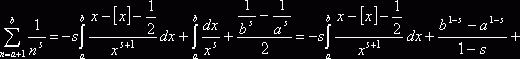
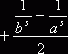 . Пусть сначала
. Пусть сначала ![]() , примем a=1, а b устремим к бесконечности. Получим
, примем a=1, а b устремим к бесконечности. Получим 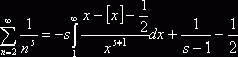 . Прибавим по единице в обе части равенств:
. Прибавим по единице в обе части равенств:
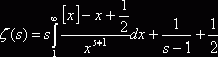 (3).
(3).
Выражение ![]() является ограниченным, так как
является ограниченным, так как ![]() , а функция
, а функция ![]() абсолютно интегрируема
на промежутке
абсолютно интегрируема
на промежутке ![]() при
при ![]() , то есть при
, то есть при ![]() ,
, ![]() . Значит, интеграл
. Значит, интеграл 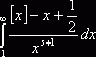 абсолютно сходится при
абсолютно сходится при
![]() , причём равномерно в любой конечной области, лежащей в
комплексной плоскости справа от прямой
, причём равномерно в любой конечной области, лежащей в
комплексной плоскости справа от прямой ![]() . Тем самым он определяет аналитическую функцию переменной s, регулярную при
. Тем самым он определяет аналитическую функцию переменной s, регулярную при ![]() . Поэтому правая часть равенства (3) представляет собой
аналитическое продолжение дзета-функции на полуплоскость
. Поэтому правая часть равенства (3) представляет собой
аналитическое продолжение дзета-функции на полуплоскость ![]() и имеет там лишь один
простой полюс в точке
и имеет там лишь один
простой полюс в точке ![]() с вычетом, равным
единице.
с вычетом, равным
единице.
Для ![]() можно преобразовать
выражение (3) дзета-функции. При
можно преобразовать
выражение (3) дзета-функции. При ![]() имеем
имеем ![]() , значит,
, значит, 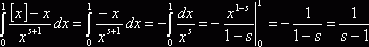 и
и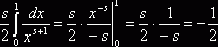 . Теперь при
. Теперь при ![]() (3) может быть
записано в виде
(3) может быть
записано в виде 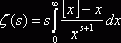 .
.
Немного более сложными рассуждениями можно установить, что в действительности (3) даёт аналитическое
продолжение дзета-функции на полуплоскость ![]() . Положим
. Положим ![]() , а
, а ![]() , то есть
, то есть ![]() первообразная для
первообразная для ![]() .
. ![]() ограничена, так как
ограничена, так как 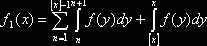 , а интеграл
, а интеграл 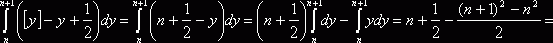
![]() и
и 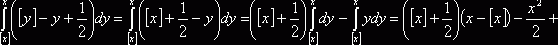
![]() ограничен из-за того, что
ограничен из-за того, что ![]() . Рассмотрим интеграл
. Рассмотрим интеграл 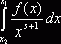 при x1>x2 и
при x1>x2 и ![]() . Проинтегрируем его по частям, приняв
. Проинтегрируем его по частям, приняв ![]() ,
, ![]() , тогда
, тогда ![]() , а по указанному выше утверждению
, а по указанному выше утверждению ![]() . Получаем
. Получаем 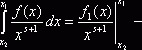
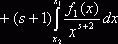 . Возьмём
. Возьмём ![]() , а
, а ![]() . Имеем
. Имеем ![]() ,
, ![]() , потому что
, потому что ![]() является ограниченной функцией. Значит,
является ограниченной функцией. Значит,
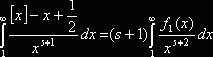 (4).
(4).
Пользуясь абсолютной сходимостью интеграла ![]() , если
, если ![]() , и ограниченностью функции
, и ограниченностью функции ![]() , делаем вывод, что в левой части равенства (4) интеграл тоже
сходится при
, делаем вывод, что в левой части равенства (4) интеграл тоже
сходится при ![]() . Значит формулой (3) можно продолжить дзета-функцию и на
полуплоскость правее прямой
. Значит формулой (3) можно продолжить дзета-функцию и на
полуплоскость правее прямой ![]() .
.
Нетрудно установить, что для отрицательных ![]()
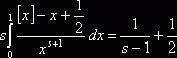 , поэтому из (3) имеем
, поэтому из (3) имеем
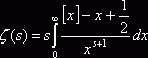 (5) при
(5) при ![]() .
.
Из теории рядов Фурье известно, что для нецелых значений x справедливо разложение в ряд
![]() (6).
(6).
Подставим его в равенство (5) и проинтегрируем ряд почленно:
Рекомендуем скачать другие рефераты по теме: bestreferat ru, реферат современная россия.
Предыдущая страница реферата | 1 2 3 4 5 | Следующая страница реферата