
Экстремумы функций многих переменных
Категория реферата: Рефераты по математике
Теги реферата: изложение по русскому 7 класс, сочинение тарас бульбо
Добавил(а) на сайт: Янкевич.
Предыдущая страница реферата | 1 2 3 4 5 6 7 | Следующая страница реферата
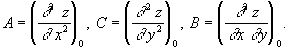
Если ![]() , то функция
, то функция ![]() имеет в точке
имеет в точке ![]() 0 и C>0 (Из условия
0 и C>0 (Из условия ![]() следует, что A и C обязательно имеют одинаковые знаки).
следует, что A и C обязательно имеют одинаковые знаки).
Если![]() , то точка
, то точка ![]() не является точкой экстремума.
не является точкой экстремума.
Если![]() , то неясно, является ли точка
, то неясно, является ли точка ![]() точкой экстремума и требуется дополнительное исследование.
точкой экстремума и требуется дополнительное исследование.
Пример:
1) Ранее в примере было установлено, что функция
![]()
имеет четыре стационарные точки:
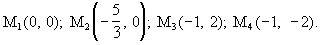
Вторые частные производные данной функции равны
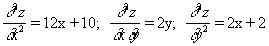
В точке ![]() имеем: A=10, B=0, C=2. Здесь
имеем: A=10, B=0, C=2. Здесь ![]() ; значит, точка
; значит, точка ![]() является точкой экстремума, и так как A и C положительны, то этот экстремум - минимум.
является точкой экстремума, и так как A и C положительны, то этот экстремум - минимум.
В точке ![]() соответственно будет A=-10, B=0, C=-4/3; .
соответственно будет A=-10, B=0, C=-4/3; .
Это точка максимума. Точки ![]() и
и ![]() не являются экстремумами функции (т.к. в них
не являются экстремумами функции (т.к. в них![]() ).
).
2) Найдем точки экстремума функции ![]() ;
;
Приравнивая частные производные нулю:
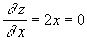 ,
, 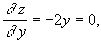
находим одну стационарную точку - начало координат. Здесь A=2, B=0, C= -2. Cледовательно, ![]() и точка (0, 0)
и точка (0, 0)
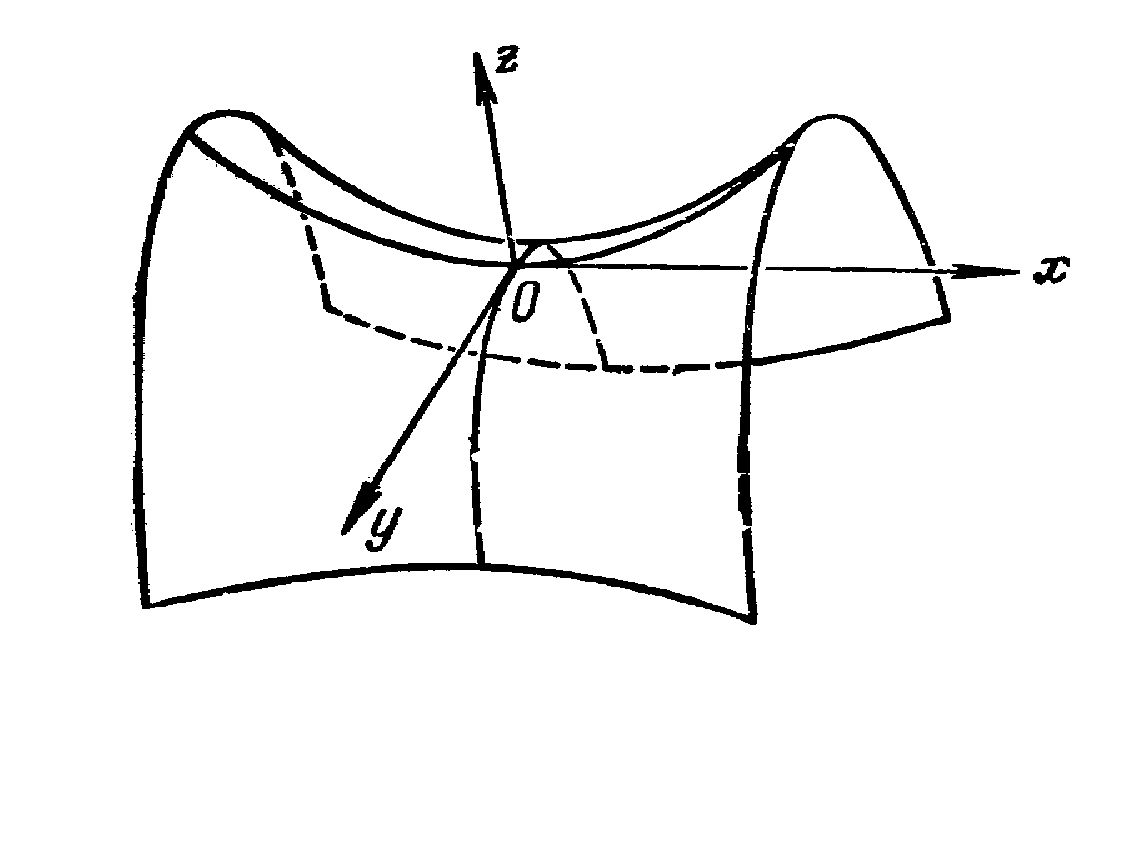
не является точкой экстремума. Уравнение ![]() есть уравнение гиперболического параболоида (см. Рис. 2.) по рисунку видно, что точка (0, 0) не является точкой экстремума.
есть уравнение гиперболического параболоида (см. Рис. 2.) по рисунку видно, что точка (0, 0) не является точкой экстремума.
Локальные Экстремумы
Определение1: Говорят, что функция ![]() имеет в точке
имеет в точке ![]() локальный максимум, если существует такая окрестность точки
локальный максимум, если существует такая окрестность точки ![]() , для которой для всякой точки M с координатами (x, y) выполняется неравенство:
, для которой для всякой точки M с координатами (x, y) выполняется неравенство: ![]() . При этом,
. При этом, ![]() т. е. приращение функции < 0.
т. е. приращение функции < 0.
Определение2: Говорят, что функция ![]() имеет в точке
имеет в точке ![]() локальный минимум, если существует такая окрестность точки
локальный минимум, если существует такая окрестность точки ![]() , для которой для всякой точки M с координатами (x, y) выполняется неравенство:
, для которой для всякой точки M с координатами (x, y) выполняется неравенство: ![]() . При этом,
. При этом, ![]() т. е. приращение функции > 0.
т. е. приращение функции > 0.
Определение 3: Точки локальных минимума и максимума называются точками экстремума.
Рекомендуем скачать другие рефераты по теме: реферат история развития, реферат на тему життя.
Предыдущая страница реферата | 1 2 3 4 5 6 7 | Следующая страница реферата