Элементарная теория сумм Гаусса

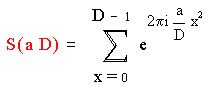
Рассмотрим следующую сумму – сумму Гаусса :

где D – целое положительное и (a, D)=1.

Покажем, что значение суммы будет одним и тем же, если х пробегает любую полную систему вычетов по модулю D.

Действительно, пусть х пробегает полную систему вычетов по модулю D. Тогда х=qD+k , где k =0, 1, …, D-1 , q є Z

Будем иметь :

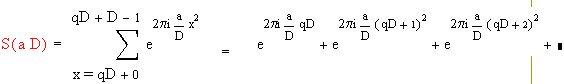
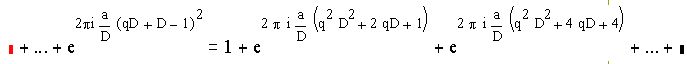
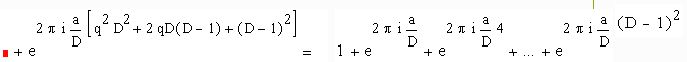
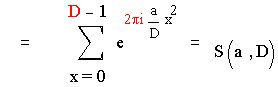
что и требовалось.

Лемма 1.

Пусть (a, D)=1. Тогда:

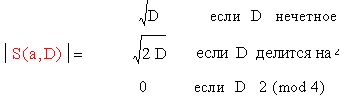
Доказательство:

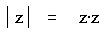
По свойству модуля комплексного числа :

Имеем:

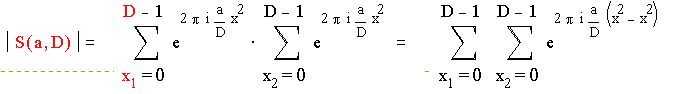
Сделаем замену x = x + t . Когда х и х пробегают полную систему вычетов по модулю D , от х и t пробегают независимо полные системы вычетов по модулю D.

Действительно, пусть х и х пробегают полную систему вычетов по модулю D . Тогда х = qD + k k=0, 1, …, D-1 , q є Z

х = pD + i i=0, 1, …, D-1 , p є Z

Следовательно, t = x – x = (q – p)D + (k – i) = l D + m , где m=0, 1, …, D-1 , l є Z

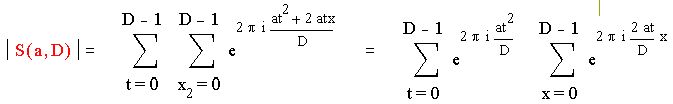
а) Пусть D – нечетное, т.е. (2а, D)=1

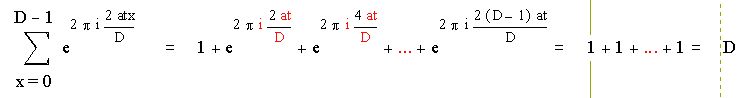
если D делит t.

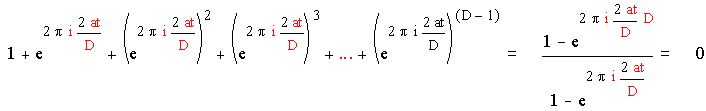
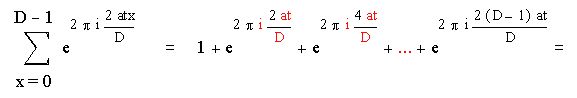
Если же D не делит t, то последнюю сумму можно записать в виде :

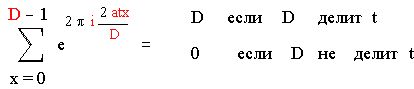
Получили :

Тогда

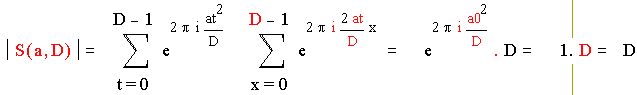
Отсюда

б) Пусть D делится на 4, т.е. возможно представление : D = 2D , где D – четное и ( a, D )=1 .

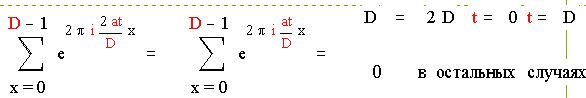
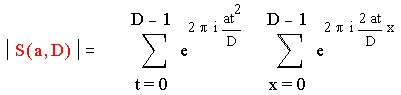
Получим :

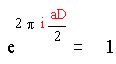
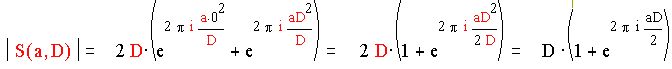
Так как D четное, то

Рекомендуем скачать другие рефераты по теме: шпоры по гражданскому праву, сообщения вконтакте.



1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки