Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

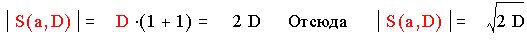
Следовательно

в) Пусть D = 2 (mod 4) , т.е. D = 4q + 2 , q є Z

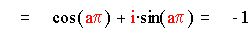
Тогда из предыдущего случая имеем : D = 2 (2q+1)= 2D , D - нечетное. Имеем :

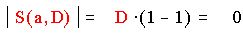
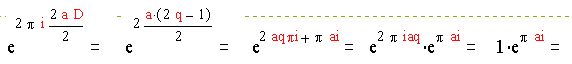
Что и требовалось.

Лемма 2.

Если D и D взаимно простые числа, то

S ( aD1 , D2 ) S ( aD2 , D1 ) = S ( a , D1 D2 )

Доказательство:

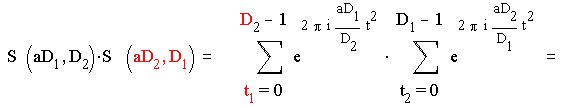
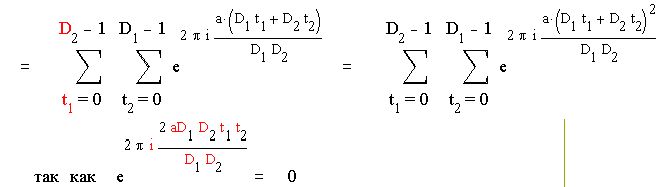
В этих суммах t1 пробегает полную систему вычетов по модулю D2 , а t2 пробегает полную систему вычетов по модулю D2. При этом D1t1 + D2t2 пробегает полную систему вычетов по модулю D1D2 . Действительно , всего членов в сумме D1D2 и никакие два несравнимы между собой. Действительно, предположим противное : пусть D1t1 + D2t2 = D1t1 + D2t2 ( mod D1D2 )

Отсюда D1 (t1 – t1) = D2 (t2 – t2 ) (mod D1D2) Тогда

D1 (t1 – t1) = D2 (t2 – t2 ) (mod D2) А так как D2 (t2 – t2 ) = 0 (mod D2)

То по свойству сравнений имеем D1 (t1 – t1) = 0 (mod D2) Отсюда так как (D1, D2)=1 , то t1 – t1 = 0 (mod D2) Аналогично получим t2 – t2 = 0 (mod D1)

Т.е. имеем t1 = t1 (mod D2) и t2 = t2 (mod D1) . Но это противоречит тому, что t1 пробегает полную систему вычетов по модулю D2 , а t2 пробегает полную систему вычетов по модулю D2, так как в полной системе вычетов любые два числа не сравнимы. Следовательно наше предположение было неверным и действительно D1t1 + D2t2 пробегает полную систему вычетов по модулю D1D2 .

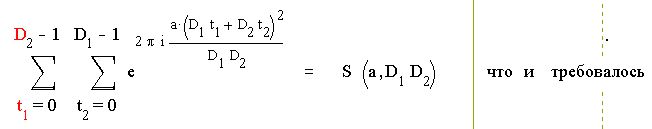
Поэтому

Лемма 3.

Пусть p простое нечетное число ине делит a . Тогда

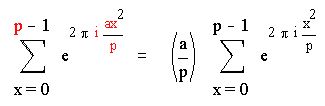
Доказательство:

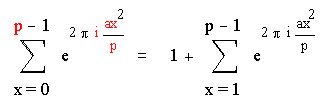
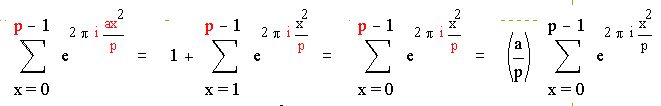
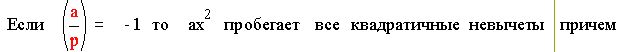
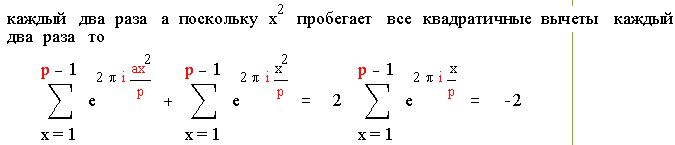
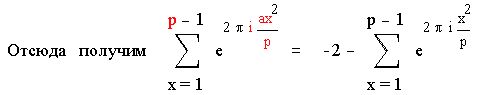
Рекомендуем скачать другие рефераты по теме: шпоры по гражданскому праву, сообщения вконтакте.



Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки