Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Вывод:[конусом назовем тело, ограниченное замкнутой конической поверхностью и пересекающей ее плоскостью].

Соглашение 2. Плоскость, пересекающая коническую поверхность назовем основанием.

Упражнение 5. Учащимся предлагается из точки S опустить перпендикуляр. Это можно сделать при помощи деревянной палочки, протянув ее в модели конуса через вершину точку S.

(а) перпендикуляр опущен в центр основания, то есть конус прямой;

б) перпендикуляр пересекает основание или плоскость основания, но не в центре, то есть наклонный конус).

Соглашение 3. Данный перпендикуляр назовем высотой конуса (кратчайшее расстояние от точки до плоскости).

Упражнение 6. Учащиеся приходят на урок с моделями по рис. 3. Необходимо выполнить полный оборот вокруг оси.

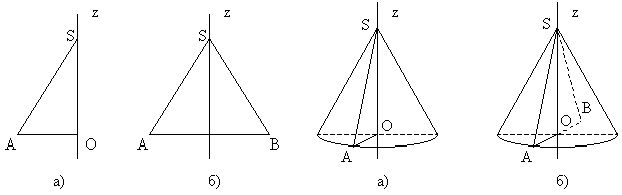
Рис.3

[поверхностью вращения. Конусом вращения назовем тело полученное при вращении прямоугольного треугольника на полный оборот вокруг одного из катетов, в тогда другой катет опишет круг основание конуса, а образующая (гипотенуза) часть конической поверхности, или равнобедренного треугольника вокруг высоты опушенной из вершины) Достаточно пол оборота].

Соглашение 4. Конус вращения – частный случай конуса, основание которого – круг и вершина проецируется в центр основания.

Изображение конуса

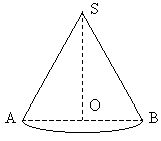
1) основание изображается в виде эллипса;

2) из точки вне плоскости основания проводятся две касательные (образующие) к концам большого диаметра эллипса.

Упражнение 7. С помощью пластилиновой модели конуса и ножа для пластилина учащимся предлагается провести всевозможные сечения конуса. Результаты систематизируются в таблицу:

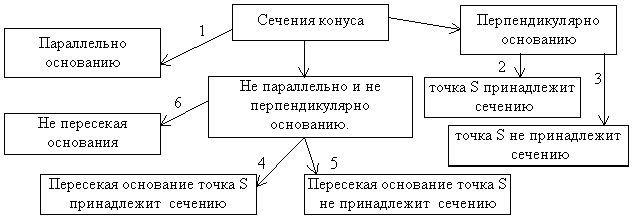
Рис.4

Соглашение 5. Конус осевое сечение (рис. 4 [2.а]) которого – равносторонний треугольник называется равносторонним конусом.

Упражнение 8. Рассмотрим часть конуса заключенную между основанием конуса и плоскостью сечения параллельной основанию (рис. 4.1.)

[эту часть конуса назовем усеченным конусом; круги с центрами в точках О и О1 – его основания; его образующие (АС, BD, …) равны между собой; прямая – ось; отрезок [ОО1] - высота].

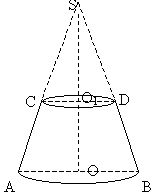
Упражнение 9. Выполните вращение следующих моделей.

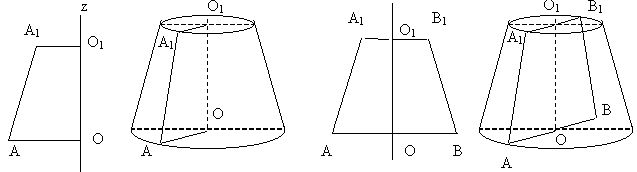
Усеченный конус можно рассматривать как тело полученное вращением прямоугольной трапеции вокруг оси, содержащей перпендикулярную сторону, или равнобокой трапеции вокруг оси симметрии.

Упражнение 10.Изобразите все возможные сечения усеченного конуса.

III этап: Введение понятия сфера и шар.

Цель этапа: Формирование понятия сфера (шар) развитие воображения, систематизация знаний по теме вращения. Формирование целостной системы.

Дидактические средства:

набор пространственных тел; пластилин; надувные шарики (круглые!); цветные карандаши; модели заготовки (рис.5).

Упражнение 1. Выполните вращение модельными заготовками. Если вращать полукруг, какое тело получится?

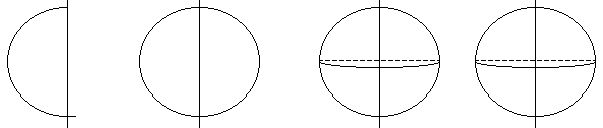
Рис. 5

Рекомендуем скачать другие рефераты по теме: защита курсовой работы, мтс сообщения.



Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки