Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

4.3.6.2. – sh2a · cos2b · cos2g – sh2a · cos2b · sin2g – sh2a · sin2b+ ch2a· cos2d + ch2a· sin2d – 1 = 0.

4.3.6.2*. – ch2a· cos2b· cos2g– ch2a· cos2b · sin2g – ch2a· sin2b · cos2d+ sh2a – ch2a · sin2b · sin2d + 1 = 0.

4.3.7. Фотон:

2.1.3.5. (X1)2 – (X2)2 – (X3)2 + (X4)2 + (X5)2 = 0 преобразовывается:

4.3.7.1. – x2 – y2 + t2 + e2 – 1 = 0.

4.3.7.1*. – x2 – y2 + t2 – e2 +1 = 0.

Тригонометрическое преобразование уравнений 4.3.7.1 и 4.3.7.1* приводит к следующему:

4.3.7.2. – sh2a· cos2b – sh2a · sin2b + ch2a · cos2d + ch2a · sin2d – 1 = 0.

4.3.7.2*. – ch2a · cos2b · cos2g – ch2a · cos2b · sin2g – ch2a · sin2b + sh2a + 1 = 0.

Уравнение 4.3.7.2 получается из уравнения 4.3.6.2 при условии g = pn/2, а уравнение 4.3.7.2* из уравнения 4.3.6.2* при условии d = pn/2. Уравнение 2.1.3.5 имеет SU(2, 3)-группу вращения.

4.3.8. Глюон:

2.1.3.3. (X1)2 – (X2)2 – (X3)2 + (X4)2 = 0 можно преобразовать:

4.3.8.1. – x2 + t2 + e2 – 1 = 0.

4.3.8.1*. – x2 + t2 – e2 +1 = 0.

4.3.8.2. – sh2a + ch2a· cos2d + ch2a · sin2d– 1 = 0.

4.3.8.2*. – ch2a · cos2b – ch2a · sin2b + sh2a + 1 = 0.

Уравнение 4.3.8.2 преобразуется из уравнения 4.1.1 при условии b = pn/2; g = pn/2, а уравнение 4.3.8.2* из уравнения 4.1.1* при условии g = pn/2; d = pn/2. Уравнения 2.1.3.3 имеют SU(2, 2) -группу вращения.

4.4. Особенности подпространств

Хотя каждое из подпространств физического пространства, в соответствии с аксиомой 1.2, не является особым, выделенным, но одновременно и не идентичным другим. Каждое из подпространств имеет свои особенности, которые мы и рассмотрим.

4.4.1. Гравитон

Важнейшей особенностью гравитационного поля является то, что оно является пространствообразующим. Оно определяет размерность наблюдаемого физического пространства (–1; 1; 1; 1) и его свойства, а все другие поля действуют в пространстве гравитационного поля. Нет для гравитации пространства (поля), внешнего по отношению к нему. Нельзя оказаться внешним по отношению к гравитационному полю. Потому любое наблюдаемое гравитационное взаимодействие есть остаточное взаимодействие внутри гравитонного потока сил типа Вандерваальсовских, а, следовательно, гравитационное взаимодействие материальных тел должно быть весьма слабым, что и наблюдается. Наблюдение гравитационного взаимодействия внутри гравитационного поля-пространства скажется и на числе степеней свободы.

Другой важнейшей особенностью гравитационного поля является налагаемый им режим квантования на все другие подпространства. Любое подпространство физического пространства имеет целочисленные отношения углов вращения, как показано выше, кроме самого гравитационного поля, естественно.

Следующей отличительной особенностью является то, что локально «пустое» пространство обладает антигравитационным эффектом, экспоненциально растущим с ростом расстояния. Это можно достаточно наглядно продемонстрировать геометрически. Если кому-либо не нравится термин – "антигравитация" – то разговор можно вести в геометрических понятиях пространств отрицательной, положительной или нулевой кривизны. Суть не изменится (напоминаем об аксиоме 1.3).

Понятие «пустого» пространства подразумевает отсутствие в нем сколько-нибудь значимых масс, зарядов, электромагнитных и прочих полей. Поместим в него тела отсчета и пробное, не способные ощутимо исказить геометрию пространства. Для свободной системы тел проекции их мировых линий в любом евклидовом сечении физического пространства будут, в общем случае, прямыми линиями. Поэтому интерес представляют гиперболические сечения (плоскости Минковского), см. рис.1.

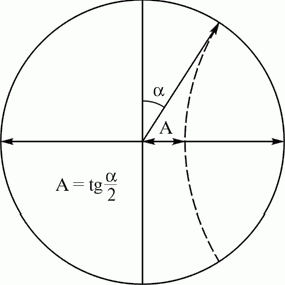
Рекомендуем скачать другие рефераты по теме: налогообложение реферат как правильно реферат, конспект урока 6 класс.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки