Предыдущая страница реферата | 1  2  3  4  5  6  7

Устранимые особые точки. Ими называются особые точки, для которых существует , где А – конечное число.

Если для особой точки существует предел , то такая особая точка называется полюсом.

Если  не существует, то точка Z=Z0 называется существенной особой точкой.

Если С-n=0, то особая точка есть устранимая особая точка.

Пусть f(Z0)=C0 и C-n  для всех  n=1,2,3,..,m отличного от 0, а для всех  n ® m+1   C-n=0, тогда Z=Z0 будет являться полюсом порядка  m.

При m>1 такой полюс будет называться простым.

, если m ® ¥ , то в этом случае в точке Z=Z0 имеем существенную особенность.

Определение 2. Вычетом функции f(Z) в круге  |Z-Z0|<R, ограничивающем изолированную особую точку Z=Z0 называется интеграл :  , где L – ориентированный против часовой стрелки контур целиком расположенный в круге радиуса R, содержащем Z0. Вычет существует только для изолированных особых точек. Очевидно, что вычет функции f(z) при Z=Z0 равен первому коэффициенту ряда главной части Лорана :

Если полюс имеет кратность m ³ 1, то для определения вычетов используется формула :

                             (3)

при m=1 :

Основная теорема о вычетах.

Пусть f(z) аналитическая в области G кроме конечного числа полюсов Z = a1, a2, …, ak. g –произвольный, кусочно-гладкий замкнутый контур содержащий внутри себя эти точки и целиком лежащий внутри области G. В этом случае интеграл  равен сумме вычетов относительно a1, a2, …, ak и т.д. умноженный на 2pi :

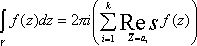                                         (5)

Пример :

Найти вычет

Особые точки : Z1=1, Z2= - 3.

Определим порядок полюсов – все полюсы первого порядка.

Используем формулу (3) :

Скачали данный реферат: Minaev, Левкин, Купцов, Мяукин, Lapotnikov, Мичуев.
Последние просмотренные рефераты на тему: матершинные частушки, сочинение рассуждение, контрольные 2 класс, биология 8 класс гдз.



Предыдущая страница реферата | 1  2  3  4  5  6  7

Поделитесь этой записью или добавьте в закладки