Предыдущая страница реферата | 1  2  3  4

(К - абсолютная константа).

Пусть 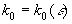- такое число, что

.

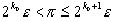Тогда для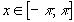

.

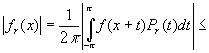
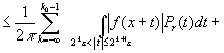
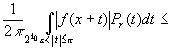
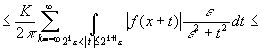
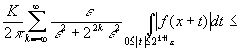
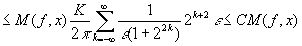Неравенство (13) доказано. Используя затем слабый тип (1,1) оператора 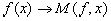, найдем такую последовательность функций 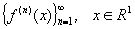,что

,

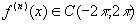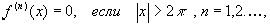( 14 )

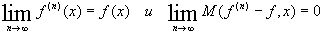для п.в. .

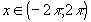Согласно (13) при xÎ (-2p , 2 p )

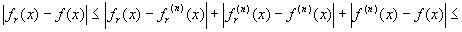
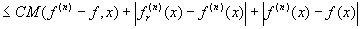
Учитывая , что по теореме 1 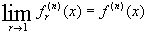для каждого xÎ [-p , p ] и (14)

Из последней оценки получим

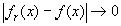при n® ¥ .

Теорема 2 доказана.

Замечание.

Используя вместо (13) более сильное неравенство (59), которое мы докажем позже, можно показать, что для п.в. xÎ [-p , p ] 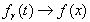, когда точка reit стремится к eix по некасательному к окружнос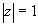ти пути.

Мы считаем , что f (x) продолжена с сохранением периодичности на отрезок [ - 2p , 2p ] (т.е. f (x) = f (y) , если x,y Î [-2p ,2p ] и x-y=2p ) и f (x) = 0 , если | x| > 2 p .

Скачали данный реферат: Kuz'minyh, Luk'jan, Нардин, Селена, Васин, Kandidij.
Последние просмотренные рефераты на тему: дипломная работа на тему, белорусские рефераты, виды рефератов, рефераты скачать бесплатно.



Предыдущая страница реферата | 1  2  3  4

Поделитесь этой записью или добавьте в закладки