Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Δyi=yi+1-yi

Δ2yi= Δyi+1- Δyi=yi+2-2yi+1+yi

………………………………

Δkyi=yi+k-kyi+1-k+k(k-1)/2!*yi+k-2+...+(-1)kyi

Будем искать интерполяционный многочлен в виде:

Pn(x)=a0+a1(x-x0)+a2(x-x0)(x-x1)+...+an(x-x0)(x-x1)...(x-xn-1)

Найдем значения коэффициентов a0, a1, a2, ...,an:

Полагая x=x0, находим a0=P(x0)=y0;

Далее подставляя значения x1, x2, ...,xn получаем:

a1=Δy0/h

a2=Δ2y0/2!h2

a3=Δ3y0/3!h3

....................

an=Δny0/n!hn

Таким образом:

Pn(x)=y0+ Δy0/h*(x-x0)+ Δ2y0/2!h2*(x-x0)(x-x1)+...+ Δny0/n!hn*(x-x0)(x-x1)...(x-xn-1)      (1)

Практически формула (1) применяется в несколько ином виде:

Возьмем: t=(x-x0)/h, тогда x=x0+th и формула (1) переписывается как:

Pn(x)=y0+tΔy0+t(t-1)/2! Δ2y0+...+t(t-1)...(t-n+1)/n!Δny0                                  (2)

Формула (2) называется интерполяционной формулой Ньютона.

Погрешность метода Ньютона оценивается следующим образом:

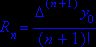
                                                        (3)

Интерполяция сплайнами.

При большом количестве узлов интерполяции сильно возрастает степень интерполяционных многочленов, что делает их неудобными для проведения вычислений.

Высокой степени многочленов можно избежать, разбив отрезок интерполирования на несколько частей, с построением в каждой части своего интерполяционного полинома. Такой метод называется интерполяцией сплайнами. Наиболее распространенным является построение на каждом отрезке [xi, xi+1], i=0..n-1 кубической функции. При этом сплайн – кусочная функция, на каждом отрезке заданная кубической функцией, является кусочно-непрерывной, вместе со своими первой и второй производной.

Будем искать кубический сплайн на каждом из частичных отрезков [xi, xi+1] в виде:

Рекомендуем скачать другие рефераты по теме: скачать доклад на тему, отчет по практике.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки