Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Где r1 = 4 (количество точек – 6, параметра – 2).

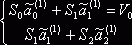Нормальная система уравнений для определения новых оценок коэффициентов функции (2.5)с помощью МНК имеет вид:

 (2.7)

Решая эту систему методом Гаусса, получим:

 (2.8)

Чем лучше функция регрессии описывает эксперимент, тем меньше для неё должна быть оценка дисперсии отдельного измерения Ui, т.к. при плохом выборе функции в дисперсию войдут связанные с этим выбором дополнительные погрешности. Поэтому для того, чтобы сделать выбор между функциями U(x) и U(1)(x) нужно проверить значимость различия между соответствующими оценками дисперсии, т.е. проверить гипотезу:

Н0 – альтернативная гипотеза

Т.е. проверить, значимо ли уменьшение дисперсии при увеличении степени многочлена.

В качестве статического критерия рассмотрим случайную величину, равную:

 (2.9)

имеющую распределение Фишера с(r ; r1) степенями свободы. Выбираем уровень распределения Фишера, находим критическое значение F*, удовлетворяющее равенству: p(F>F*=

В нашем случае F=349.02, а F*=10,13.

Если бы выполнилось практически невозможное соотношение F>F, имевшее вероятность 0,01, то гипотезу Н0 пришлось бы отклонить. Но в нашем случае можно ограничиться многочленом

, коэффициенты в котором неодинаковы.

3. Нахождение коэффициента теплопроводности .

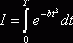 Коэффициент вычислим по формуле (1.5), обозначим:

 (3.1)

Определим допустимую абсолютную погрешность величины интеграла I, исходя из требования, чтобы относительная погрешность вычисления не превосходила 0,1%, т.е.:

 (3.2)

Т.к. из (3.1) очевидно, что , то условие (3.2) заведомо будет выполнено, если:

 (3.3)

Т.е. в качестве предельно допустимой абсолютной погрешности вычисления интеграла I возьмём 0,001Т (3.4)

Т=218 оС, следовательно, 0,218 оС.

3.1 Вычисление интеграла I методом трапеции

 Использование теоретической оценки погрешности

Для обозначения требуемой точности количества частей n, на которые нужно разбить отрезок интегрирования [0;T] определяется по формуле:

Рекомендуем скачать другие рефераты по теме: реферат по труду, педагогические рефераты.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки