Комбинаторные формулы

Пусть имеется множество, состоящее из n элементов. Обозначим его . Перестановкой из n элементов называется заданный порядок во множестве .

Примеры перестановок:

1)распределение n различных должностей среди n человек;

2)расположение n различных предметов в одном ряду.

Сколько различных перестановок можно образовать во множестве? Число перестановок обозначается Pn (читается “Р из n”).

Чтобы вывести формулу числа перестановок, представим себе n ячеек, пронумерованных числами 1,2,...n. Все перестановки будем образовывать, располагая элементы Un в этих ячейках. В первую ячейку можно занести любой из n элементов (иначе: первую ячейку можно заполнить n различными способами). Заполнив первую ячейку, можно найти n–1 вариантов заполнения второй ячейки. Таким образом, существует n(n–1) вариантов заполнения двух первых ячеек. При заполнении первых двух ячеек можно найти n–2 варианта заполнения третьей ячейки, откуда получается, что три ячейки можно заполнить n(n-1)(n-2) способами. Продолжая этот процесс, получим, что число способов заполнения n ячеек равно . Отсюда

   Pn = n(n – 1)(n – 2)...×3×2×1

Число n(n – 1)(n – 2)...×3×2×1, то есть произведение всех натуральных чисел от 1 до n, называется "n-факториал" и обозначается n! Отсюда Pn =n!

По определению считается: 1!=1; 0!=1.

Пример. Сколько существует вариантов замещения 5-ти различных вакантных должностей 5-ю кандидатами?

    .

Размещениями из n элементов по k элементов будем называть упорядоченные подмножества, состоящие из k элементов множества   (множества, состоящего из n элементов). Число размещений из n элементов по k элементов обозначается  (читается "А из n по k").

Одно размещение из n элементов по k элементов может отличаться от другого как набором элементов, так и порядком их расположения.

Примеры задач, приводящих к необходимости подсчета числа размещений

1) Сколькими способами можно выбрать из 15 человек 5 кандидатов и назначить их на 5 различных должностей?

2) Сколькими способами можно из 20 книг отобрать 12 и расставить их в ряд на полке?

В задачах о размещениях полагается k<n. В случае, если k=n, то легко получить

Для подсчета  используем тот же метод, что использовался для подсчета Pn, только здесь возьмем лишь k ячеек. Первую ячейку можно заполнить n способами, вторую, при заполненной первой, можно заполнить n–1 способами. Таким образом, существует п(п–1) вариантов заполнения первых двух ячеек. Можно продолжать этот процесс до заполнения последней k–й ячейки. Эту ячейку при заполненных первых k–1 ячейках можно заполнить
 n–(k–1) (или n–k+1) способами. Таким образом, все k ячеек заполняются числом способов, равным

  

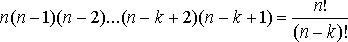
Отсюда получаем:

Пример. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов для поездки в 4 различных страны?

  

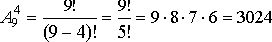
Сочетаниями из n элементов по k элементов называются подмножества, состоящие из k элементов множества  (множества, состоящего из n элементов).

Одно сочетание от другого отличается только составом выбранных элементов (но не порядком их расположения, как у размещений).

Число сочетаний из n элементов по k элементов обозначается  (читается "C из n по k").

Рекомендуем скачать другие рефераты по теме: тесты онлайн, реферат машины.



1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки