Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Примеры задач, приводящих к подсчету числа сочетаний:

1) Сколько существует вариантов выбора 6-ти человек из 15 кандидатов для назначения на работу в одинаковых должностях?

2) Сколькими способами можно из 20 книг отобрать 12 книг?

Выведем формулу для подсчета числа сочетаний. Пусть имеется множество  и нужно образовать упорядоченное подмножество множества , содержащее k элементов (то есть образовать размещение). Делаем это так:

 1) выделим какие-либо k элементов из n элементов множества  Это, согласно сказанному выше, можно сделать  способами;

 2) упорядочим выделенные k элементов, что можно сделать  способами. Всего можно получить  вариантов (упорядоченных подмножеств), откуда следует:  , то есть

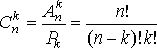          (1)

Пример: 6 человек из 15 можно выбрать числом способов, равным

  

Несложно понять, что осуществить выбор подмножества из т элементов множества, насчитывающего п элементов, можно, выбрав п–т элементов, которые не войдут в интересующее нас подмножество. Отсюда следует свойство числа сочетаний

  

Эту формулу можно доказать, используя формулу (1).

Задачи на подсчет числа подмножеств конечного множества называются комбинаторными. Рассмотрим некоторые комбинаторные задачи.

1.Из семи заводов организация должна выбрать три для размещения трех различных заказов. Сколькими способами можно разместить заказы?

Так как из условия ясно, что каждый завод может либо получить один заказ, либо не получить ни одного, и что выбрав три завода, можно по-разному разместить среди них заказы, здесь нужно считать число размещений

  

2.Если из текста задачи 1 убрать условие различия трех заказов, сохранив все остальные условия, получим другую задачу. Теперь способ размещения заказов определяется только выбором тройки заводов, так как все эти заводы получат одинаковые заказы, и число вариантов определяется как число сочетаний.

  

3.Имеются 7 заводов. Сколькими способами организация может разместить на них три различных производственных заказа? (Заказ нельзя дробить, то есть распределять его на нескольких заводах).

В отличие от условия первой задачи, здесь организация может отдать все три заказа первому заводу или, например, отдать два заказа второму заводу, а один - седьмому.

Задача решается так. Первый заказ может быть помещен семью различными способами (на первом заводе, на втором и т.д.). Поместив первый заказ, имеем семь вариантов помещения второго (иначе, каждый способ помещения первого заказа может сопровождаться семью способами помещения второго). Таким образом, существует 7×7=49 способов размещения первых двух заказов. Разместив их каким-либо образом, можем найти 7 вариантов помещения третьего (иначе, каждый способ размещения первых двух заказов может сопровождаться семью различными способами помещения третьего заказа). Следовательно, существуют 49×7=73 способов размещения трех заказов. (Если бы заказов было n, то получилось бы 7n  способов размещения).

4.Как решать задачу 3, если в ее тексте вместо слов "различных производственных заказа" поставить "одинаковых производственных заказа"? Это трудная задача. Ниже приводится аналогичная задача– Задача V с решением.

5.Добавим к условию задачи 1 одну фразу: организация также должна распределить три различных заказа на изготовление деревянных перекрытий среди 4-х лесопилок. Сколькими способами могут быть распределены все заказы?

Каждый из  способов распределения заказов на заводах может сопровождаться  способами размещения заказов на лесопилках. Общее число возможных способов размещения всех заказов будет равно

  

Рекомендуем скачать другие рефераты по теме: тесты онлайн, реферат машины.



Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки