Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Пример 2. Решить неравенство: .

Освободимся от знаменателей, для чего умножим обе части неравенства на положительное число 6, оставив без изменения знак неравенства.

, далее последовательно получаем ; .

Последнее неравенство верно при любом значении х, так как при любом значении переменной х получается истинное высказывание 0>-55. Поэтому множеством его решений служит вся числовая прямая.

Ответ: (-¥; +¥).

Пример 3. Решить неравенство: ½х-1½<3.

На основании определения модуля данное неравенство запишем в виде совокупности двух систем неравенств

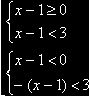   (1)                (2)

решая эту совокупность получим (2), таким образом решением этого неравенства является промежуток (-2; 4).

Пример 4. Решить неравенство:½х+1½>2-х.

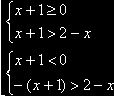
отсюда х>0,5 из первой системы, а вторая система – не имеет решения.

Ответ: (0,5; +¥)

5. Система и совокупности неравенств.

Говорят, что несколько неравенств с одной переменной образуют систему, если ставится задача найти множество общих решений заданных неравенств.

Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называется решением системы неравенств.

Множество решений системы неравенств есть пересечение множеств решений неравенств, образующих систему. Неравенства, образующие систему, объединяются фигурной скобкой.

Например:  

Иногда используется запись в виде двойного неравенства. Например, систему неравенств  можно записать в виде двойного неравенства .

Говорят, что несколько неравенств с одной переменной образуют совокупность, если ставится задача найти множество таких решений, каждое из которых является решением хотя бы одного из этих неравенств.

Значение переменной, при котором хотя бы одно из неравенств, образующих совокупность, обращается в верное числовое неравенство, называется решением совокупности неравенств.

Множество решений совокупности неравенств есть объединение множеств решений неравенств, образующих совокупность. Неравенства, образующие совокупность, иногда объединяются квадратной скобкой. Так, запись  означает, что неравенства образуют совокупность.

Пример 1. Решить систему неравенств:    Û   

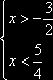
                       х

С помощью числовой прямой находим, что пересечением этих множеств служит интервал . Это и есть множество решений данной системы.

Рекомендуем скачать другие рефераты по теме: скачать дипломную работу на тему, матершинные частушки.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки