Рефераты | Рефераты по математике | Линейные уравнения и неравенства | страница реферата 7 | Большая Энциклопедия Рефератов от А до Я
Большая Энциклопедия Рефератов от А до Я
  • Рефераты, курсовые, шпаргалки, сочинения, изложения
  • Дипломы, диссертации, решебники, рассказы, тезисы
  • Конспекты, отчеты, доклады, контрольные работы


    • Рефераты | Рефераты по математике | Линейные уравнения и неравенства


    Рефераты | Рефераты по математике | Линейные уравнения и неравенства

    Линейные уравнения и неравенства




    Категория реферата: Рефераты по математике
    Теги реферата: инновационная деятельность, реферат анализ
    Добавил(а) на сайт: Альвина.



    Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 |



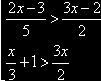
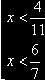
    Пример 2. Решить совокупность неравенств:Рефераты | Рефераты по математике | Линейные уравнения и неравенства

    Рефераты | Рефераты по математике | Линейные уравнения и неравенстваПреобразовав каждое из неравенств, получим совокупность, равносильную данной Рефераты | Рефераты по математике | Линейные уравнения и неравенства

                   Рефераты | Рефераты по математике | Линейные уравнения и неравенства       Рефераты | Рефераты по математике | Линейные уравнения и неравенства     х

    Объединением этих множеств служит промежуток Рефераты | Рефераты по математике | Линейные уравнения и неравенства, который и является решением совокупности неравенств.

    6. Неравенства и системы неравенств с двумя переменными.

    Известно, что пара действительных чисел (х0; у0) однозначно определяет точку координатной плоскости. Это дает возможность изображать множество решений неравенства или системы неравенств с двумя переменными геометрически, в виде некоторого множества точек координатной плоскости.

    Пример 1. Дать геометрическую интерпретацию решения неравенства Рефераты | Рефераты по математике | Линейные уравнения и неравенства.

    Преобразуем данное неравенство к виду Рефераты | Рефераты по математике | Линейные уравнения и неравенства.

    Построим в прямоугольной системе координат прямую Рефераты | Рефераты по математике | Линейные уравнения и неравенства.

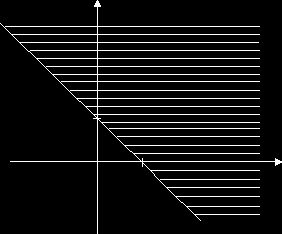
    Так как ордината любой точки, лежащей выше прямой Рефераты | Рефераты по математике | Линейные уравнения и неравенства, больше, чем ордината точки, лежащей на прямой и имеющей такую же абсциссу, то множество точек плоскости, расположенных выше этой прямой и служит геометрической интерпретацией решения заданного неравенства.

    Рефераты | Рефераты по математике | Линейные уравнения и неравенства       у

         1

    х

                    Рефераты | Рефераты по математике | Линейные уравнения и неравенства

    Геометрическая интерпретация позволяет записать решение в виде

    Рефераты | Рефераты по математике | Линейные уравнения и неравенства   или   Рефераты | Рефераты по математике | Линейные уравнения и неравенства 

    (для составления второй записи нужно преобразовать уравнение Рефераты | Рефераты по математике | Линейные уравнения и неравенства к виду, разрешенному относительно х).

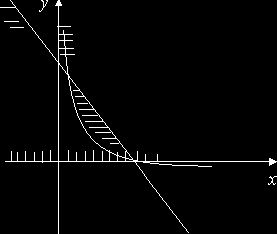
    Пример 2. Решить систему неравенств: 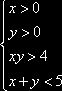Рефераты | Рефераты по математике | Линейные уравнения и неравенства

    Найдем на координатной плоскости пересечение областей Рефераты | Рефераты по математике | Линейные уравнения и неравенства, получим геометрическое решение заданной системы неравенств.

    Рефераты | Рефераты по математике | Линейные уравнения и неравенства

    Рефераты | Рефераты по математике | Линейные уравнения и неравенстваРефераты | Рефераты по математике | Линейные уравнения и неравенства 

    у= -х+5

    (1; 4)
     

    у=Рефераты | Рефераты по математике | Линейные уравнения и неравенства


    Рекомендуем скачать другие рефераты по теме: скачать дипломную работу на тему, матершинные частушки.



    Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 |




    Поделитесь этой записью или добавьте в закладки

       

    Категории:



    Разделы сайта




    •