Математическое моделирование нестационарного электрического поля анодной защиты
Категория реферата: Рефераты по математике
Теги реферата: сочинение 3, диплом
Добавил(а) на сайт: Нелли.
Предыдущая страница реферата | 1 2 3 4 5 | Следующая страница реферата
Катодная поляризационная кривая описывается функцией:
|
Jk( |
(5) |
)=k1[exp(k2где k1, k2 - константы, определяемые по экспериментальным данным.
Для описания анодных поляризационных кривых предложена функция:
|
х |
(6) |
где a1, ..., a4 - константы, определяемые по экспериментальным данным; V - скорость развертки напряжения.
Таким образом, для уравнения (1) сформулированы граничные условия: на катодах - (3), (5); на анодах - (4), (6); на изоляторах -
|
j(p)=0, |
p |
(7) |
Характеризующий коррозионные потери суммарный электрический заряд Q, проходящий через защищаемые поверхности Sa за время tp, определяется интегралом:
|
|
q |
(8) |
Если ставить задачу минимизации коррозионных потерь при пуске анодной защиты, то оптимальными в этом смысле следует считать такое количество и расположение катодов, при которых для выбранной скорости V электрический заряд Q, определяемый интегралом (8), минимален.
Вопросы численной реализации
Задача (1)-(7) решалась в трех- и двумерных областях для емкостей различной геометрии. Распределение потенциала определялось решением нелинейного интегрального уравнения, построенного на основе формулы Грина [9], которую с учетом (1) можно записать в виде:
|
|
(9) |
,где
p, q
S; 
=(m–1)
, m -
размерность задачи; G(p, q)=1/R(p, q) при m=3, G(p, q)= –ln[R(p, q)] при m=2;
R(p, q) - расстояние между точками p и q. Из формулы (9) с учетом (2) получено
интегральное уравнение:
|
|
,
для решения которого применяется итерационная процедура:
|
Рекомендуем скачать другие рефераты по теме: доклад на тему язык, компьютерные рефераты. Предыдущая страница реферата | 1 2 3 4 5 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |
,
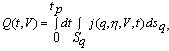
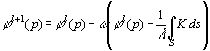