Рефераты | Рефераты по математике | Математическое моделирование нестационарного электрического поля анодной защиты Математическое моделирование нестационарного электрического поля анодной защиты Категория реферата: Рефераты по математике Теги реферата: сочинение 3, диплом Добавил(а) на сайт: Нелли. Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

(11)

где l - номер итерации; ядро K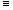K [p, q, 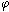(q)] определяется соотношениями:

При выбранной скорости V счет проводился по времени t от 0 до tmax, при этом напряжение увеличивалось от 0 до Umax=V tmax. Затем знак V менялся на противоположный, t уменьшалось от tmax до 2 tmax, напряжение - от Umax до 0. По результатам расчета определялись границы пассивной зоны (U1, U2) и напряжение U, соответствующее минимальной плотности тока. Далее по формуле (8) определялся общий заряд пуска.

Итерационный процесс (11) оценивался по условию 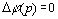для всех pS. При выполнении очередного цикла итераций (11) для каждого t контролировалось выполнение балансового соотношения по току с относительной погрешностью  1 %.

Для определения параметров в формулах (5), (6) были использованы данные, приведенные в [6] для стали 18 % Cr – 8 % Ni в 1N H2SO4 при 250 C. При этом получены значения параметров: k1=0.04315, k2=17.25, a1=350, a2=0.3, a3=17, a4=0.3.

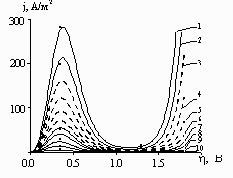
Рис. 1. Анодные поляризационные зависимости, построенные по формуле (6) для скоростей V, В/час: 1 – 720; 2 – 360; 3 – 180; 4 – 90; 5 – 45; 6 – 22,5; 7 – 12; 8 – 6; 9 – 1,6; 10 – 0,4; 11 – 0,025. Точками обозначены экспериментальные данные для скоростей V, В/час: 720; 360; 12; 6; 1,6; 0,4; 0,025.

На рис. 1 представлены анодные поляризационные зависимости j(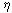), построенные по формуле (6). Сплошной линией выделены кривые, для которых экспериментальные данные [6] при тех же значениях скорости V нанесены точками. Точки выбраны из трех участков: 1) участка максимальной плотности тока в области активного растворения; 2) переходного участка; 3) участка пассивного состояния анода. Из рисунка видно, что предложенная зависимость (6) качественно согласуется с экспериментальными данными в исследуемом диапазоне значений скорости развертки потенциала.

Результаты расчетов

Приведем некоторые результаты численных расчетов пусковых режимов анодной защиты стального цилиндра, заполненного серной кислотой и защищаемого одним цилиндрическим катодом (рис. 2).

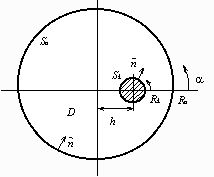
Рис. 2. Схема электрохимической системы. Sa – защищаемая поверхность; Sk – поверхность катода; Ra, Rk – радиусы анода и катода; h – расстояние между центрами электродов;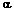,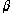– углы отсчета граничных точек на аноде и катоде; – нормаль к границе.

Радиусы границ имеют значения: Ra=10 см, Rk=2 см; электропроводность среды 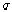=10 см/м. Расстояние между центрами границ h изменялось от 0 до 7 см. Напряжение U изменялось от 0 до Umax=2.4 В, затем обратно от Umax до 0.

На рис. 3 представлены зависимости потенциала в различных точках анода (а) и катода (б) от приложенного напряжения при скорости пуска V=36 В/час. Стрелками указаны решения при прямой и обратной развертке напряжения. На участке U1<U2<U3 наблюдаются два решения: верхнее соответствует активному растворению, нижнее - пассивному состоянию анода. Из рисунка видно, что для достижения пассивного состояния анода (U=U) необходимо вначале увеличивать напряжение U от 0 до U2 (верхняя ветвь графика), а затем уменьшать от U2 до U (нижняя ветвь). Волна пассивации перемещается по поверхности анода от точки 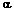=0 к удаленной точке 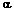=, при этом защитный потенциал 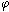возрастает (от линии 1 к линии 4).

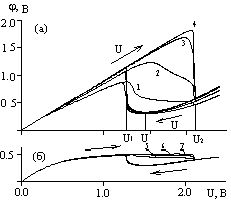
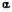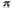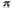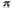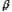Рис. 3. Зависимость потенциала от приложенного напряжения при h=5 см; V=36 В/час на аноде (а) при углах, равных, рад: 1 – 0; 2 –/3; 3 – 2 /3; 4 –; и на катоде (б) при углах, равных, рад: 5 – 0; 6 –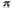/2; 7 –  .

В табл. 1 приведены параметры пассивной зоны (U1, U2) при различных расстояниях h между центрами границ. Из таблицы видно, что с увеличением h меняется ширина пассивной зоны, причем наименьшее значение (0.6) соответствует h=3.

Таблица 1. Интервал пассивной зоны при различных расстояниях h между центрами электродов

Главная | Партнеры | Лучшие рефераты

Обратная связь

Рефераты | Рефераты по математике | Математическое моделирование нестационарного электрического поля анодной защиты | страница реферата 3 | Большая Энциклопедия Рефератов от А до Я    Все рефераты, курсовые, дипломы, шпаргалки, сочинения, изложения, решебники, конспекты являются общедоступными    Копирование и размещение в интернете разрешается только при наличии активной индексируемой ссылки на Ahaha.ru

© 2006-2020 «Ahaha.ru»