Методы и алгоритмы построения элементов систем статистического моделирования Содержание

Введение

1. Метод статистического моделирования систем

2. Моделирование случайных величин и процессов

3. Основные понятия марковских процессов

4. Математический аппарат дискретных марковских цепей

Введение

В настоящее время нельзя назвать область человеческой деятельности, в которой в той или иной степени не использовались бы методы моделирования. Особенно это относится к сфере управления различными системами, где основными являются процессы принятия решений на основе получаемой информации.

Метод моделирования широко применяют в таких областях, как автоматизация проектирования и организации в автоматизированных системах научных исследований, в системах исследования и проектирования, в системах массового обслуживания, анализ различных сторон деятельности человека, автоматизированное управление производственными и другими процессами. Важно подчеркнуть, что моделирование используется при проектировании, создании, внедрении, эксплуатации систем, а также на различных уровнях их изучения, начиная от анализа работы элементов и кончая исследованием системы в целом при их взаимодействии с окружающей средой.

1. Метод статистического моделирования систем

На этапе исследования и проектирования систем при построении и реализации машинных моделей (аналитических и имитационных) широко используется метод статистического моделирования (Монте-Карло), который базируется на использовании случайных чисел, т.е. возможных значений некоторой случайной величины с заданным распределением вероятностей. Статистическое моделирование представляет собой метод получения с помощью ЭВМ статистических данных о процессах, происходящих в моделируемой системе. Для получения представляющих интерес оценки характеристик моделируемой системы S с учетом воздействий внешней среды Е статистические данные обрабатываются и классифицируются с использованием методов математической статистики,

Сущность метода статистического моделирования сводится к построению для процесса функционирования исследуемой системы S некоторого моделирующего алгоритма, имитирующего поведение и взаимодействие элементов системы с учетом случайных входных воздействий и воздействий внешней среды Е, и реализации этого алгоритма с использованием программно-технических средств ЭВМ.

Различают две области применения метода статистического моделирования:

для изучения стохастических систем; для решения детерминированных задач.

Основной идеей, которая используется для решения детерминированных задач методом статистического моделирования, является замена детерминированной задачи эквивалентной схемой некоторой стохастической системы, выходные характеристики последней совпадают с результатом решения детерминированной задачи. При такой замене погрешность уменьшается с увеличением числа испытаний (реализации моделирующего алгоритма) N.

В результате статистического моделирования системы S получается серия частных значений искомых величин или функций, статистическая обработка которых позволяет получить сведения о поведении реального объекта или процесса в произвольные моменты времени. Если количество реализации N достаточно велико, то полученные результаты моделирования системы приобретают статистическую устойчивость и с достаточной точностью могут быть приняты в качестве оценок искомых характеристик процесса функционирования системы S.

При статистическом моделировании систем одним из основных вопросов является учет стохастических воздействий. Количество случайных чисел, используемых для получения статистически устойчивой оценки характеристики процесса функционирования системы S при реализации моделирующего алгоритма на ЭВМ, колеблется в достаточно широких пределах в зависимости от класса объекта моделирования, вида оцениваемых характеристик, необходимой точности и достоверности результатов моделирования. Для метода статистического моделирования на ЭВМ характерно, что большое число операций, а соответственно большая доля машинного времени расходуются на действия со случайными числами. Кроме того, результаты статистического моделирования существенно зависят от качества исходных (базовых) последовательностей случайных чисел. Поэтому наличие простых и экономичных способов формирования последовательностей случайных чисел требуемого качества во многом определяет возможность практического использования машинного моделирования системы.

Понятие “статистическое моделирование” тесно связано с понятием “метод Монте-Карло” и почти ему тождественно.

Для решения задач методом Монте-Карло необходимо получать на ЭВМ последовательность выборочных значений случайной величины с заданным распределением. Такой процесс принято называть моделированием случайной величины. Случайные величины обычно моделируют с помощью преобразований одного или нескольких независимых значений случайной величины а, равномерно распределенной в интервале (0,1). Независимые случайные величины, равномерно распределенные в интервале (0,1).

Можно выделить следующие этапы моделирования случайных величин:

генерирование N реализации случайной величины с требуемой функцией распределения; преобразование полученной величины, определяемой математической моделью; статистическая обработка реализации.

Особенностью первого этапа является то, что все методы для получения заданного распределения используют преобразование равномерно распределенной величины.

Конструктивно задаются случайная величина, равномерно распределенная в интервале (0,1), 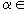(0,l), далее производится отображение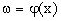 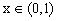и получается новая случайная величина 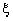с распределением, определяемым решаемой задачей, в общем случае 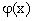может быть довольно сложным.

Далее следует получение некоторых характеристик. При параметрических оценках вычисляется некоторая функция 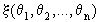. При непараметрическом задании функций распределения обычно вычисляются плотности или функции распределения. Чаще всего находят оценки математической ожидания. Погрешность оценки определяется дисперсией (если она известна) по числу экспериментов N.

В результате можно выделить следующие этапы (рис. 4.1):

подготовка исходных данных (блок 1), генерирование равномерно распределенных случайных чисел (блок 2), преобразования для получения заданного закона распределения (блок 3); выполнение дополнительных преобразований в соответствии с проблем ной областью (блок 4); статистическая обработка (блок 5).

Рис. 4.1. Технологический процесс в Монте-Карло системах

где:

- ПИД - подготовка исходных данных,

- ГРРСЧ - генерирование равномерно распределенных случайных чисел;

- ГПЗ - генерирование произвольного (заданного) закона распределения;

Рекомендуем скачать другие рефераты по теме: налоги в россии, бесплатные тесты бесплатно.



1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки