Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

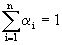(14)

Тогда любое из уравнений в (8.14) можно исключить.

Так же, как и в случае поглощения ДМЦ многие характеристики эргодических цепей определяются с помощью фундаментальной матрицы, которая в этом случае будет иметь вид:

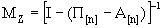(15)

Для эргодических цепей характеристикой, имеющей важное практическое значение, является продолжительность времени, за которое процесс из состояния 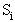впервые попадает в 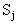, так называемое время первого достижения. Матрица средних времен достижения определяется по формуле:

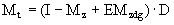(16)

где

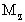- фундаментальная матрица (15);

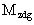- диагональная матрица, образованная из фундаментальной заменой всех элементов, кроме диагональных, нулями;

D - диагональная матрица с диагональными элементами, ;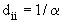

Е - матрица, все элементы которой равны единице.

Матрица дисперсий времени первого достижения имеет несколько более сложный вид:

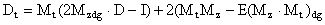(17)

где кроме уже упомянутых обозначений встречается новое - (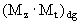, обозначающее диагональную матрицу, полученную из матричного произведения матриц .

4.3. Управляемые марковские цепи

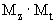Как указывалось выше, под управляемыми марковскими процессами понимают такие, у которых имеется возможность до определенной степени управлять значениями переходных вероятностей. В качестве примеров таких процессов можно привести любые торговые операции, у которых вероятность сбыта и получения эффекта может зависеть от рекламы, мероприятий по улучшению качества, выбора покупателя или рынка сбыта и т.д.

Очевидно, что при создании математических моделей в данном случае должны фигурировать следующие компоненты:

конечное множество решений (альтернатив)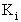 , где 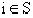- номер состояния системы; матрицы переходов 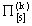соответствующие тому или иному принятому k-му решению; матрицы доходов (расходов) 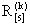, также отражающие эффективность данного решения.

Управляемой цепью Маркова (УЦМ) называется случайный процесс, обладающий марковским свойством и включающий в качестве элемента математической модели конструкцию (кортеж) 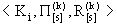. Решение, принимаемое в каждый конкретный момент (шаг процесса), назовем частным управлением.

Таким образом, процесс функционирования системы, описываемой УЦМ, выглядит следующим образом:

если система находится в состоянии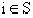 и принимается решение 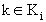, то она получает доход 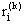; состояние системы в последующий момент времени (шаг) определяется вероятностью 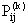, то есть существует вероятность того, что система из состояния 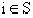перейдет в состояние 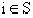, если выбрано решение .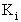

Очевидно, общий доход за n шагов является случайной величиной, зависящей от начального состояния и качества принимаемых в течение хода процесса решений, причем это качество оценивается величиной среднего суммарного дохода (при конечном времени) или среднего дохода за единицу времени (при бесконечном времени).

Стратегией p называется последовательность решений:

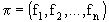(18)

где

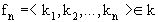- вектор управления.

Задание стратегии означает полное описание конкретных решений, принимаемых на всех шагах процесса в зависимости от состояния, в котором находится в этот момент процесс.

Если в последовательности (векторе) p все 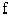одинаковы, то такая стратегия называется стационарной, т.е. не зависящей от номера шага. Стратегия 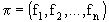называется марковской, если решение 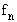, принимаемое в каждом конкретном состоянии, зависит только от момента времени n, но не зависит от предшествующих состояний.

Рекомендуем скачать другие рефераты по теме: налоги в россии, бесплатные тесты бесплатно.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки