Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

.

ТЕМА 3. Векторное произведение векторов. Смешанное произведение трех векторов. ПРАВАЯ И ЛЕВАЯ ТРОЙКИ ВЕКТОРОВ

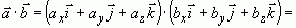
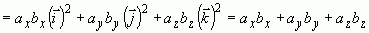Линейно независимые векторы 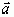, 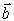и 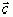образуют правую тройку векторов, если они имеют такую же ориентацию, как соответственно большой, указательный и средний палец правой руки, в противном случае говорят о левой тройке векторов

Три единичных вектора i, j, k, попарно ортогональные друг другу и образующие правую тройку векторов, называют прямоугольной декартовой системой координат.

Углом между векторам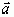и и 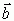называют такой угол a , не превосходящий p , на который нужно повернуть вектор 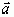, чтобы совместить его с направлением вектора 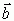, начало которого должно совпадать с началом 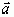.Угол между векторами обозначается (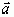,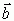) или (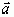Ù ).

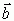ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.

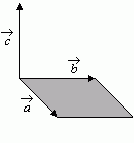
Под векторным произведением векторов 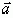и 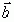понимают вектор 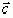, имеющий длину и направленный перпендикулярно к плоскости 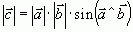,определяемой векторам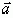и и 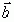, причем так, что векторы 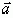,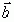и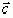 образуют правую тройку векторов (длина вектора 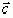численно равна площади параллелограмма, построенного на векторах 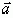и 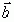как на сторонах (это геометрический смысл векторного произведения).

Векторное произведение обозначают: 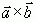или 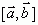. Очевидно, что 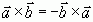(из определения векторного произведения). 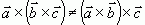. Векторное произведение подчиняется только распределительному закону:

.

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ТРЕХ ВЕКТОРОВ

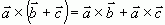Смешанным произведением векторов 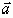, 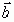и 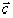назовем число К, равное объему параллелепипеда, построенного на этих векторах (рис. 10) и вычисляемое как:

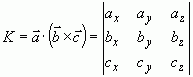
Очевидно, что есл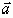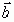и , и 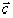компланарны, то К = 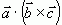=0.

Из определения смешанного произведения следует интересный факт, что произведение не зависит от порядка следования векторов в смешанном произведении, так как объем параллелепипеда (положительный или отрицательный) зависит только от расположения этих векторов в пространстве (левая или правая тройка) потому, что является псевдоскаляром. Следовательно, можно записать

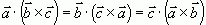или .

Это свойство смешанного произведения служит обоснованием упрощения записи смешанного произведения:

.

ТЕМА 4. Прямая линия на плоскости. УРАВНЕНИЕ ПРЯМОЙ НА ПЛОСКОСТИ

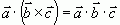На плоскости, заметим, могут быть заданы только двухмерные, или плоские преобразования.

Уравнение 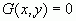, связывающее две переменные x и y называется уравнением линии L в выбранной плоской системе координат, если координаты любой точки этой линии L удовлетворяют уравнению, а любые другие координаты точек, не принадлежащих лини L, не удовлетворяют указанному уравнению.

По определению линия — это есть соотношение, связывающее координаты точек некоторой области пространства, и, причем только эти координаты. Уравнение представляет собой аналитическую запись уравнения любой плоской линии.

.

УРАВНЕНИЕ ПРЯМОЙ С ЗАДАННОЙ ТОЧКОЙ И НАПРАВЛЯЮЩИМ ВЕКТОРОМ

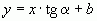Если вместо 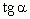подставить его численное значение, от получим известное уравнение прямой

.

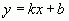Известно, что уравнение прямой имеет вид:

.

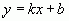По условию задачи k задан. Точка M (x0 ,y0) должна также принадлежать искомой прямой и, по определению линии, обращать уравнение прямой в тождество. Воспользуемся этим и подставим значения x0 и y0 в уравнение, получим :

.

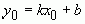Рекомендуем скачать другие рефераты по теме: шпора на пятке лечение, персонал реферат.



Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки