Предыдущая страница реферата | 1  2  3  4  5  6

Пример 2. 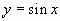; ; 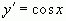; ; 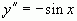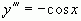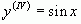. Так как 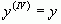, то можно предположить, что в данном случае функцию можно дифференцировать бесконечное количество раз.

Пример 3. 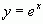. . 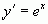Как и во втором примере, эта функция дифференцируема бесконечное количество раз.

Пример 4. 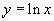. 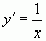; ; 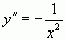; 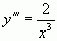… ; 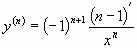...Как следует из приведенных примеров, разные функции ведут себя по-разному при многократном дифференцировании. Одни имеют конечное количество производных высших порядков, другие – переходят сами в себя, а третьи, хотя и дифференцируемы бесконечное количество раз, но порождают новые функции, отличные от исходной. Однако все сформулированные теоремы о производных первых порядков выполняются для производных высших порядков.

ТЕМА 9. Экстремум функции. ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИЙ

Функция называется возрастающей на некотором промежутке 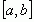, если на этом промежутке большему значению независимой переменной соответствует большее значение функции, т.е. есл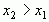и и 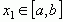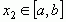, то выполняется .

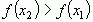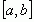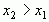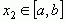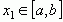Функция называется убывающей на некотором промежутке , если на этом промежутке большему значению независимой переменной соответствует меньшее значение функции, т.е. если и , , то .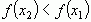

Если функция определима и непрерывна на некотором отрезке 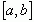и на концах отрезка имеет знак, то на указанном отрезке эта функция имеет по крайне мере хотя бы одну точку, в которой .

ЭКСТРЕМУМ ФУНКЦИИ

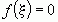Функция 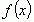достигает своего максимума в точке 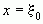, если ее значение в окрестности этой точки меньше, чем значение функции в этой же точке .

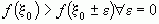Функция 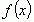достигает своего минимума в точке 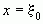, если ее значение в окрестности этой точки больше, чем значение функции в этой же точке .

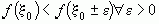Правило поиска экстремальных точек

1. Находим область определения функции .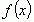

2. Находим производную функции .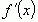

3. Определяем критические точки 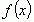по ее первой производной.

4. Исследуем 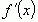на знак слева и справа от найденных точек.

5. Если слева от точки 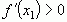, а справа 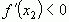, то тогда говорят, что точка 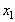является точкой максимума.

6. Если слева от точки 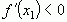, а справа 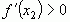, то тогда говорят, что точка 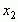является точкой минимума.

7. Если 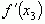слева и справа от критической точки не меняет знак, то говорят, что 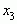является точкой перегиба функции.

Если функци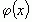и и 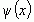непрерывны при 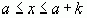, где 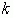– некоторое положительное число, отличное от нуля и достаточно маленькое, и имеют непрерывные производные в указанной точке, а также 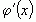не обращается в нуль при вычитании указанных условий, тогда можно сформулировать следующую теорему.

ПРАВИЛО ЛОПИТАЛЯ

Теорема Коши. Если при соблюдении предположений относительно функци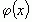й и 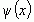отношение 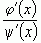стремится к некоторому числу при 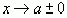, то тогда к такому же числу будет стремиться отношение функций .

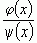Эта теорема позволяет формулировать правило Лопиталя. При раскрытии неопределенности вида 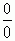можно функцию числителя 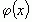и знаменателя 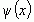заменить их производным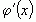и и 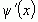, соответственно, и рассматривать предел 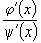вместо 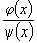в указанной точке.

Скачали данный реферат: Arsentij, Privalov, Rozenbah, Станислава, Благово, Burcov.
Последние просмотренные рефераты на тему: конспект зима, ответы школа, доклад на тему культура, реферат по математике.



Предыдущая страница реферата | 1  2  3  4  5  6

Поделитесь этой записью или добавьте в закладки