Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

Т.е.

т.к.

т.к.

Из чего следует, что если уравнение задано в виде соотношения для действия на искомый вектор оператора "rot" , то из этого уравнения можно получить в качестве решения только вихревой вектор как интеграл по замкнутому контуру.

Если задано уравнение в виде действия на вектор операторов "div" или "grad div" , то из этого уравнения можно получить в качестве решения только скаляр или вектор градиентного поля.

Приложение полученных результатов исследования классической теории поля к системе уравнений электродинамики Максвелла

Рассмотрим полную систему уравнений электродинамики Максвелла для электрических и магнитных полей в вакууме с позиции основных положений классической теории поля. С этой целью перепишем полную систему уравнений для электрических и магнитных полей.

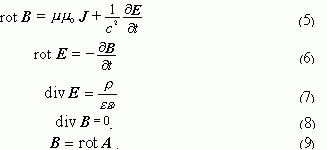
С позиции классической теории поля:

1) вектор магнитной индукции B представлен в уравнениях (5;6;8;9) данной системы уравнений, из которых видно, что вектор B носит строго вихревой характер (6;8;9), и его источники (возбудители) в исследуемом пространстве заданы уравнением (5). Т.е. поле вектора B соответствует основной задаче теории поля и может быть однозначно получено как решение данной системы уравнений после подстановки соответствующих краевых и начальных условий;

2) вектор напряженности электрического поля E, согласно уравнениям (6) и (7) данной системы, имеет отличные от нуля и дивергенцию, и ротор и, следовательно, имеет отличные от нуля вихревую и градиентную составляющие. Т.е., должен быть представлен в общем виде согласно теореме Гельмгольца (с изменением знака перед потенциальной частью):

E = - grad j + rot P ;

и

где P - некий векторный потенциал вихревой составляющей электрического поля, физический смысл которого будет выяснен дальше.

Анализируя уравнения (5) и (6), приходим к выводу, что они дают соотношения для действий оператора " rot " на векторы полей B и E , и, как было показано ранее, нетривиальные решения этих уравнений можно получить только для векторов вихревых полей. Но, т.к. вектор E имеет и вихревую, и градиентную составляющие, то решением уравнений (5) и (6) может быть только вихревая составляющая вектора E, т.е. rotP. градиентная составляющая вектора E может быть определена только из уравнения (7). Но, очевидно, уравнение (7) описывает только статические электрические поля или поля, распространяющиеся с бесконечной скоростью, что лишено всякого физического смысла. Отсюда следует, что система уравнений электродинамики Максвелла не содержит в себе описание нестационарных градиентных электрических полей и механизма их распространения.

Для того, чтобы убедиться в правильности подобных рассуждений, проделаем весь путь традиционного метода решения системы уравнений электродинамики.

Решение системы уравнений электродинамики

Подставим в уравнение (5) системы уравнений электродинамики вектор E в общем виде:

Рекомендуем скачать другие рефераты по теме: конспект 2 класс, ответы по контрольной.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки