|
14
|
|
Функции с разрывом в точке
экстремума
|
-
|
1
|
-
|
-
|
1
|
|
Функции, немонотонные в
окрестности точки экстремума
|
-
|
-
|
-
|
2
|
2
|
Одним
из стандартных и наиболее распространенных упражнений при изучении понятия
"экстремум функции" является задание исследовать указанную функцию на
наличие экстремума. Таблица №1 показывает, что количество таких заданий
невелико: в задачнике [3] содержится 10 упражнений, чуть больше в задачниках
[1] и [2] - 17 и 16 соответственно, наибольшее количество упражнений содержится
в задачнике [5]. Уже на первом этапе анализа можно сказать, что при
использовании традиционных задачников невозможна дифференциация и, тем более, индивидуализация обучения. Действительно, даже 28 упражнений недостаточно для
составления индивидуальных заданий для группы в 20-25 человек, тем более, если
учесть необходимость охвата данными упражнениями экстремумов разных типов.
Серия
примеров из §1 показывает, что непрерывность функции в точке экстремума, дифференцируемость функции в точке экстремума, монотонность функции в
односторонней открытой окрестности точки экстремума не являются ни
необходимыми, ни достаточными условиями наличия экстремума. Во избежание
возникновения и упрочения упрощенных представлений о сути понятия экстремума в
упражнениях должны быть представлены функции, обладающие различными сочетаниями
свойств в точке экстремума и ее окрестностях. Рассматриваемые задачники не
отличаются большим разнообразием в данном отношении. Так, §9 задачника [2]
содержит только одну функцию с разрывом в точке экстремума (№314.2) и три
функции, не дифференцируемые в точке экстремума (№№ 303.2, 308.2, 309.2), одна
из которых является модификацией функции 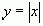 , а две другие
- модификациями функции
, а две другие
- модификациями функции 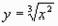 . В задачниках
[3] и [1] все предлагаемые функции непрерывны в точках экстремума, а не
дифференцируемых среди них две (№107 б,д) и четыре (№№ 1171, 1174, 1177, 1196)
соответственно. И вновь недифференцируемые функции являются модификациями
функций
. В задачниках
[3] и [1] все предлагаемые функции непрерывны в точках экстремума, а не
дифференцируемых среди них две (№107 б,д) и четыре (№№ 1171, 1174, 1177, 1196)
соответственно. И вновь недифференцируемые функции являются модификациями
функций 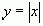 и
и 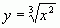 . Необходимо
отметить, что в выше рассмотренных задачниках [1,2,3] все функции монотонны в
открытых односторонних окрестностях экстремальных точек. В задачнике [5]
содержится пять функций, не дифференцируемых в точке экстремума (№№ 1421, 1422, 1427, 1428, 1444), и нет ни одной функции с разрывом в точке экстремума. В
дополнение к стандартным примерам недифференцируемых функций в №1444
предлагается исследовать функцию
. Необходимо
отметить, что в выше рассмотренных задачниках [1,2,3] все функции монотонны в
открытых односторонних окрестностях экстремальных точек. В задачнике [5]
содержится пять функций, не дифференцируемых в точке экстремума (№№ 1421, 1422, 1427, 1428, 1444), и нет ни одной функции с разрывом в точке экстремума. В
дополнение к стандартным примерам недифференцируемых функций в №1444
предлагается исследовать функцию 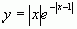 . Также в
данном задачнике приведены три функции, немонотонные в односторонних открытых
окрестностях точки экстремума (№№ 1427, 1428). Ни в одном из задачников не
представлены функции, построенные на основе простейших неэлементарных функций
. Также в
данном задачнике приведены три функции, немонотонные в односторонних открытых
окрестностях точки экстремума (№№ 1427, 1428). Ни в одном из задачников не
представлены функции, построенные на основе простейших неэлементарных функций  ,
, 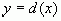 ,
, 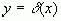 .
.
Приведенный
анализ выявляет два обстоятельства. Во-первых, функции с подобными
"экзотическими" экстремумами весьма немногочисленны, однообразны и
рассеяны по разным задачникам. Даже будучи собранными вместе, они не образуют
педагогически значимого подмножества, на основе которого можно было бы провести
углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями
математического анализа. Во-вторых, объективно получается, что традиционные
коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания.
Этого вполне достаточно, если рассматривать задачник как инструмент для
выработки технических навыков, сопутствующих лекционному курсу, и отнюдь
недостаточно, если требовать от задачника выполнения более сложных функций, как
это делается, например, в монографии А.В.Ястребова [11.C.38].
Как
было сказано выше, желательно, чтобы при решении упражнений восстанавливались
какие-либо утраченные навыки. При отыскании экстремумов дифференцируемых в
области определения функций учащийся сталкивается с необходимостью решить
уравнение 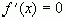 . Возникает
естественная возможность повторить методы решения основных типов уравнений, известных учащимся. В школе учащиеся изучают следующие типы уравнений:
рациональные, дробно-рациональные, иррациональные, тригонометрические, показательные, логарифмические, трансцендентные, уравнения с параметрами и со
знаком модуля.
. Возникает
естественная возможность повторить методы решения основных типов уравнений, известных учащимся. В школе учащиеся изучают следующие типы уравнений:
рациональные, дробно-рациональные, иррациональные, тригонометрические, показательные, логарифмические, трансцендентные, уравнения с параметрами и со
знаком модуля.
Таблица
№2
