Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

 Причем и здесь можно выразить эти многочлены через многочлены Чебышева – Лагерра , а условие ортогональности будет:

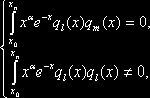           если

Полиномы Якоби.

Предположим, что многочлен (2) имеет два различных действительных нуля. Тогда , и уравнение Пирсона (1) представимо в виде

,

где  и  - некоторые постоянные и . Тогда решение уравнения (1)

 представимо в виде

 и определяет некоторую систему ортогональных многочленов, которая линейным преобразованием независимого переменного и умножением на постоянную сводится к системе многочленов Якоби . Так как весовая функция многочленов Якоби имеет вид

.

И соответственно условие ортогональности будет иметь вид:

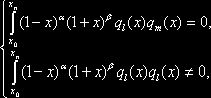       если

Многочлены Чебышева I рода являются частным случаем многочленов Якоби, так как весовая функция, относительно которой ортогональны эти многочлены, имеет вид:

и получается при подстановке в весовую функцию многочленов Якоби параметров .

Многочлены Чебышева II рода так же являются частным случаем многочленов Якоби, так как весовая функция многочленов Чебышева II рода имеет вид

и получается при подстановке в весовую функцию многочленов Якоби параметров .

Следует так же отметить, что многочлены Лежандра являются частным случаем многочленов Якоби, так как весовая функция многочленов Лежандра

 и есть частный случай весовой функции многочленов Якоби при .

Глава 3. Примеры нахождения кривых распределения вероятностей и программное обеспечение.

В этой главе рассматриваются примеры нахождения кривых распределения по методу кривых Пирсона с использованием теоретических исследований, рассмотренных в первой и второй главах дипломной работы. Было написано программное обеспечение, с помощью которого были получены и проинтерпретированы численные результаты.

§ 1. Примеры нахождения кривых распределения вероятностей.

Рассмотрение примеров заключалось в том, что было рассмотрено пятьдесят случайных выборок, а далее были рассмотрены примеры выборок с заданным законом распределения. Согласно рассмотренному ниже алгоритму были произведены соответствующие вычисления, и по каждой выборке была построена кривая распределения вероятностей. При проведении испытаний было получено, что кривая распределения сорока семи из пятидесяти рассмотренных выборок есть кривая Пирсона первого типа, которая определяется следующей формулой:

Рекомендуем скачать другие рефераты по теме: решебник по 5, темы рефератов по физике.



Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки