Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата

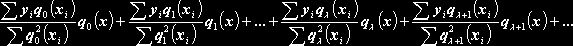
Этот ряд, обладающий свойством давать посредством суммы своих первых членов приближенное представление интерполируемой функции в виде целой функции степени , удовлетворяющей требованию наименьших квадратов, называется интерполяционным рядом Чебышева.

Теперь для полного решения задачи остается еще узнать, что представляют собой функции , определив через данные величины  и  коэффициенты при  в выражении этих функций.

Далее, с помощью разложения дроби

по нисходящим степеням  получим, что дробь

,

где

,

дает приближенное представление функции [7]

 с точностью до членов степени

включительно. Здесь  есть весовая функция, найденная ранее по методу Пирсона. Но эта дробь, у которой степень числителя на единицу меньше степени знаменателя, при разложении в непрерывную дробь всегда будет в своих неполных частных содержать переменную  в первой степени. Следовательно, знаменатели ее подходящих дробей есть функции степеней ; поэтому можно положить

.

 Что касается , то его можно приравнять .

Разлагая

 в непрерывную дробь вида

,

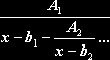 где  и  - некоторые постоянные, используем найденные выше свойства функции  для определения этих постоянных через данные значения .

Выражения для  будет иметь вид:

.

Выражения для коэффициентов  будут следующими:

.

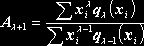Рекомендуем скачать другие рефераты по теме: решебник по 5, темы рефератов по физике.



Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки