Отображение геометрических структур
Категория реферата: Рефераты по математике
Теги реферата: оценка дипломной работы, питание реферат
Добавил(а) на сайт: Ruf'.
1 2 | Следующая страница реферата
Отображение геометрических структур
ABSTRACT
Mapping geometrical arrangements of a fiber space of differential equations, bound mapping of Hopf-Colle is under construction.
Устанавливается изоморфизм отображений Хопфа-Коула (Hopf E, Cole J. D.) [ 1, 2 3 ] и отображений геометрических структур дифференциальных уравнений, что позволяет определить сферы действия геометрического исчисления с соответствующей метрикой. Эта сфера действия соответствующих метрик определяется линейными и нелинейными связями.
Имеется проблема.
В настоящее время геометрии искривленных пространств позволяют извлекать физическую информацию в основном о системах космических и галактических масштабов: релятивистская теория гравитации (ОТО) и новая релятивистская теория гравитации (РТГ), в которых определяется «метрический тензор риманового пространства».
Но геометрия – раздел математики. Геометрическое исчисление имеет силу во всех разделах физики. Примером может служить интегральное исчисление, которое широко используется во всех разделах физики.
С помощью метрического тензора опускают и поднимают индексы у тензоров, находят их абсолютные переносы, определяют ковариантные производные и связности… Итак, посредством определенных в ОТО и РТГ метрических тензоров дважды поднимаются индексы, например, у тензора диэлектрической проницаемости в электродинамике, определяется перенос составляющих вектора электрической напряженности. Каков физический смысл этих действий? Ведь метрические тензоры в ОТО и РТГ – это гравитационные потенциалы!
В материальном мире реализуются многомерные пространства. С каждой физической системой и с каждым процессом ассоциируются соответствующей структуры пространства. Введение многомерных расслоенных пространств возможно во всех разделах физики. И не просто возможно, а геометрии расслоенных пространств составляют основу теорий всех разделов физики.
Геометрические действия с соответствующей метрикой возможно только в рамках соответствующей связи. При переходе к другой связи посредством соответствующих отображений происходит переход и к другой метрике посредством этих же отображений. Введение тензоров (скаляров, спиноров, векторов, тензоров более высокого ранга) производится только относительно соответствующих преобразований обобщенных координат. В физике вводятся многомерные пространства внутренних степеней свободы. Примером пространства внутренних степеней свободы в физике может служить изотопическое пространство, векторы в котором вводятся на основе преобразований координат изотопического пространства. В пространстве внутренних степеней свободы вводятся обобщенные базовые и слоевые координаты.
В качестве демонстрации данных утверждений и рассматривается сформулированная здесь задача.
Отображение Хопфа-Коула связывает два дифференциальных уравнения и их решения [ 1, 2, 3 ]: нелинейное уравнение Бюргерса [ 4 ] и уравнение теплопроводности (диффузии). Эти уравнения отображают соответствующие связи. Этих уравнений мы рассматриваем частные случаи (демонстрируется сам принцип) и обобщаем их на слоевые пространства.
Нелинейное уравнение (3) (см. Табл.) получено из уравнения типа уравнения Бюргерса в классе решений
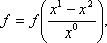т.е. 
(1)
с использованием отображения (2) [ 5 ]:
Отображение геометрических структур Таблица|
Дифференциальное уравнение типа уравнения теплопроводности
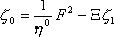
Рекомендуем скачать другие рефераты по теме: сочинение капитанская, здоровый образ реферат. 1 2 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |
(3)
-постоянные.
- длина вектора
в пространстве 
- постоянная интегрирования.
(5)
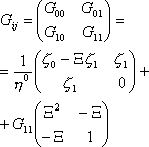(10)
(12) 
(5’)