
Отображение геометрических структур
Категория реферата: Рефераты по математике
Теги реферата: оценка дипломной работы, питание реферат
Добавил(а) на сайт: Ruf'.
Предыдущая страница реферата | 1 2
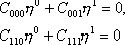
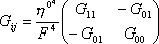
Рефераты | Рефераты по математике | Отображение геометрических структур
Отображение геометрических структурКатегория реферата: Рефераты по математике Теги реферата: оценка дипломной работы, питание реферат Добавил(а) на сайт: Ruf'. Предыдущая страница реферата | 1 2
|
Дифференциальные уравнения, связанные отображением Хопфа-Коула
|
Уравнение, следующее из нелинейного дифференциального уравнения типа уравнения Бюргерса
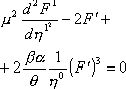
|
|
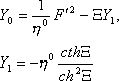 (9)
(9)
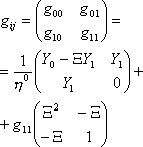
(11)
![]()
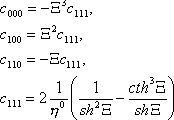 (13)
(13)
![]() (6’)
(6’)
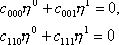 )
)
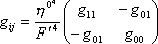
Из Таблицы следует, что структура составляющих контравариантных векторов, метрического
тензора, связностей сохраняется. Изменяется их конкретное содержание. Отображения Хопфа-Коула меняют длину слоевых координат ![]() . Поскольку выполняется условие Эйлера и сохраняется свойство (14),то коэффициенты связностей найдены правильно. Итак, 1)если связь задана
дифференциальным уравнением вида (3), тогда следует проводить геометрическое исчисление с метрическим тензором (10) и метрикой (5), 2)если же связь задана
нелинейным дифференциальным уравнением вида (4), тогда следует проводить геометрическое исчисление
с метрическим тензором (11) и метрикой (6), которые могут быть получены отображением Хопфа-Коула (2).
. Поскольку выполняется условие Эйлера и сохраняется свойство (14),то коэффициенты связностей найдены правильно. Итак, 1)если связь задана
дифференциальным уравнением вида (3), тогда следует проводить геометрическое исчисление с метрическим тензором (10) и метрикой (5), 2)если же связь задана
нелинейным дифференциальным уравнением вида (4), тогда следует проводить геометрическое исчисление
с метрическим тензором (11) и метрикой (6), которые могут быть получены отображением Хопфа-Коула (2).
ЛИТЕРАТУРА
1.Cole J.D. On a quasilinear parabolic equation occurring in aerodynamics/ Quart App. Vath.,1951, 9, pp. 225-236.
2.Hopf T. The partial differential equation ![]() Comm. Pure
Appl.Math.,1950, pp/ 201-230.
Comm. Pure
Appl.Math.,1950, pp/ 201-230.
3.Абловиц М., Сигур X. Солитоны и метод обратной задачи. Перевод с англ. -М.: Мир, 1987, 180 с.
4.Burgers J. M. A mathematical model illustrating the theory of turbulence/Adv. Appl. Mech, 1948, 1, pp. 171-199.
5.Севрюк В.П. Геометрии расслоенных пространств теории обобщенных криволинейных координат. ВИНИТИ , N 3378-B90 Деп., 145 с.