Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Q+W=λjWj

Q-W=μjWj

dλj=λkWjk+14(λjμk-λkμj)Wk+λjkWk

dμj=μkWjk+14(λjμk-λkμj)Wk+μjkWk (4)

λjk=(14(μαλjk-λαμjk)+116λkμα(μj-λj)+λjkα)Wα

μjk=(14(μαλjk-λαμjk)+116λkμα(μj-λj)+μjkα)Wα

Из уравнений (4) вытекает, что система величин Г2={λj,μj,λjk,μjk} образует геометрический объект. Он называется фундаментальным геометрическим объектом второго порядка отображения f. Дальнейшее продолжение системы (2) приведет к фундаментальному геометрическому объекту ГР порядка р :

ГР={λj,μj,λj1j2,μj1j2,...,λj1j2...jp,μj1j2...jp}.

§ 4. Векторы и ковекторы первого порядка.

Из системы дифференциальных уравнений (5) вытекает, что система величин {λj},{μj} образует подобъекты геометрического объекта Г1. Будем называть их основными ковекторами 1-го порядка. Основные ковекторы определяют для каждой точки P две инвариантные прямые:

λjXj=1 ; μjXj=1 (6)

не инцидентные точке Р. Из условия rang f=2 и уравнения (2) вытекает, что прямые (6) не параллельны. Условия (*) показывают, что величины {λj,μj} являются компонентами матрицы ,обратной к матрице, составленной из координат основных ковекторов. Таким образом , величины {λj,μj} охватываются объектом Г1.

Из (*) получаем:

dλj=-λkWkj-14(λj+μj)μtWt-λktλkλtWt-μktWt^λkμj

dμj=-μkWkj-λktμkλjWt-μktμkμjWt+14λt(λj+μj)Wt

Таким образом , система величин и образуют геометрические объекты, охваченные объектом Г1. Будем называть их основными векторами 1-го порядка.

Предположение 1.Конец вектора v1=λjej (вектора v2=μjej) лежит на прямой (6). Доказательство вытекает из формул (*),(2). Прямые, параллельные прямым (6), инцидентные точке Р, определяются соответственно уравнениями:

λjXj=0 , μjXj = 0 (7).

Предположение 2. Основные векторы {λj} и {μj} параллельны прямым (6) соответственно. Доказательство вытекает из формул (*) и (7). Взаимное расположение рассмотренных векторов и прямых представлено на рисунке:

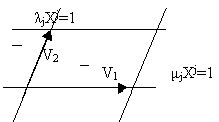
Система величин ρj=λj-μj образует ковектор: dρj=ρkWjk+(μjk-λjk)Wk.

Определяемая им прямая ρjXj=0 (8) проходит через точку Р и точку пересечения прямых (6).

Пусть W-однородное подмногообразие в R(p1,p2) содержащее элементы (р1,р2) определяемое условием: (р1*,р2*)∈W↔p1*p2*=p1p2.

Теорема 1.Прямая (8) является касательной в точке Р к прообразу f-1(W) многообразия W при отображении f.

Доказательство:

Рекомендуем скачать другие рефераты по теме: собственность реферат, шпаргалки бесплатно скачать.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки