Применение движений к решению задач

Бычек В. И., доцент кафедры геометрии ХГПУ

Рассмотрим применение простейших движений[1] плоскости, таких как параллельный перенос, симметрия и вращение (поворот) при решении задач элементарной геометрии на вычисление и доказательство.

При решении задач используются основные свойства движения. Так, всякое движение переводит:

прямую в прямую, а параллельные прямые – в параллельные прямые,

отрезок – в отрезок, а середину отрезка – в середину отрезка,

луч – в луч,

угол – в равный ему угол,

точки, не лежащие на одной прямой – в точки, не лежащие на одной прямой,

полуплоскость – в полуплоскость.

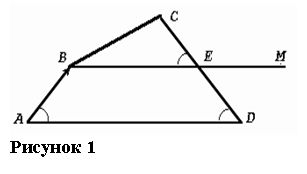
ЗАДАЧА 1.

В четырехугольнике ABCD (рис.1) AB = , BC = 3, CD = 2, Ð BAD = ÐCDA = 60°. Найти углы ABC и BCD.

Решение. Рассмотрим параллельный перенос на вектор  .

Получим равнобедренную трапецию ABED, у которой AB = ED = , а ÐABE =120°. Тогда CE = CD – ED = .

В треугольнике BCE имеем 9 = x2 + 3 – 2xCos60° (по теореме косинусов), где BE = x.

Отсюда x2 - x  - 6 = 0 и x = 2. Замечая, что BE2 = BC2 + CE2, получим ÐBCD = 90°, а ÐCBE = 30°. Тогда ÐABC = 120° + 30° = 150°.

ЗАДАЧА 2.

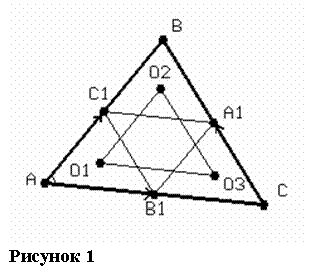
Пусть A1, B1, C1 – середины сторон треугольника ABC (рис.2), O1, О2, O3 – центры окружностей, вписанных в треугольники AC1B1, C1BA1, СВА1. Найти углы треугольника O1O2O3, если AB = 4, AC = 4, ÐBAC = 30°.

Решение.

Сначала по теореме косинусов найдем сторону BC треугольника ABC: BC=4.

Следовательно, треугольник ABC будет равнобедренным и ÐBCA=30°. Рассмотрим параллельный перенос на вектор. Так как:A®B1, B1®C, C1®A1, то  отображает треугольник AB1C1 в треугольник B1CA1. Тогда :O1®O3. Отсюда следует, что O1O3||AC. Аналогично рассмотрим параллельный перенос на вектори параллельный перенос на вектор .

:O1®O2Þ O1O2||AB, :O3®O2ÞO2O3||BC.

Тогда ÐO2O1O3=ÐBAC=30° , ÐO1O3O2 =Ð BCA = 30°, а ÐO3O2O1=180°-2×30°=120°.

ЗАДАЧА 3.

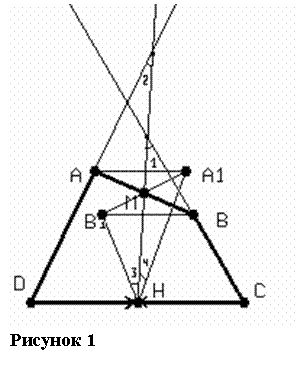Прямая, проходящая через середины сторон AB и CD четырехугольника ABCD, не являющего трапецией, образует со сторонами AD и CD равные углы. Доказать, что AD = CB.

Рекомендуем скачать другие рефераты по теме: курсовые, реферат на тему ресурсы.



1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки