Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Решение.

Пусть M и H – середины сторон AB и CD (рис.3). Рассмотрим сначала параллельный перенос на вектор  и параллельный перенос на вектор .  : D ®H, A ®A1,Þ AD||A1H, AD = A1H; :C® H, B®B1 Þ BC ||B1H, BC=B1H. Так как по условию Ð1=Ð2, а Ð1 =Ð3 и Ð2=Ð4 как накрестлежащие углы, то Ð3=Ð4.

Затем рассмотрим центральную симметрию относительно точки M. Так как ZM : A®B, то луч AA1 отобразится в луч BB1 , так как AA1 ||BB1||DC. ZM : A1®B1, так как AA1 = DH = HC = BB1. В треугольнике A1B1H медиана MH является биссектрисой. Следовательно, треугольник A1B1H равнобедренный, т. е. A1H=B1H. Тогда и AB = CB.

ЗАДАЧА 4.

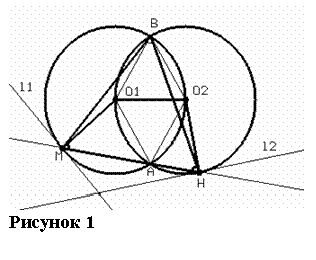
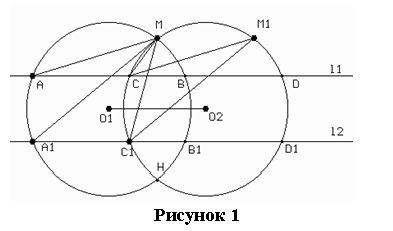Даны две окружности b1(O1, r) и b2 (O2, r), пересекающиеся в точках M и H (рис.4). Прямая i, параллельная прямой O1O2, пресекает окружность b1 в точках A и B , а окружность b2 в точках C и D . Доказать, что величина угла AMC не зависит от положения прямой i, если лучи AB и CD сонаправлены и прямая i пересекает отрезок MH.

Решение.

Пусть прямая i1 также удовлетворяет условиям задачи. Докажем, что ÐAMC=ÐA1MC1. Так как ÐAMC=ÐAMA1+ÐA1MC, а ÐA1MC1=ÐA1MC+ÐCMC1 то надо доказать, что ÐAMА1 =ÐСMC1 . Рассмотрим параллельный перенос на вектор . :b1(O1,r) ®b2(O2,r). Тогда :M®M1, A®C, A1®C1. Значит :ÐAMA1®ÐCM1C1. Следовательно, ÐAMA1=ÐCM1C1. Но ÐCM1C1=ÐCMC1 как вписанные углы, опирающиеся на одну и ту же дугу CC1. Тогда ÐAMA1=ÐCMC1=ÐAMC=ÐA1MC1.

ЗАДАЧА 5.

Доказать, что точки, симметричные ортоцентру треугольника ABC относительно прямых AB, AC, BC, принадлежат описанной около треугольника ABC окружности.

Решение.

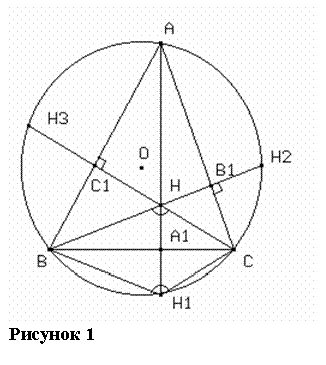
Пусть окружность b(O,r) описана около треугольника ABC, а H – его ортоцентр, т. е. H – точка пересечения высот треугольника ABC (рис.5). Рассмотрим осевую симметрию относительно прямой BC. SBC : B®B, C®C, H®H1. Значит SBC: CH®CH1, BH®BH1, ÐСHB®ÐCH1B. Следовательно, ÐСHB =ÐСH1B. Так как в четырехугольнике AC1HB1

ÐAC1H=ÐAB1H=90°, то ÐBAC+ÐС1HB1=180°. Тогда в четырехугольнике ABH1C имеем ÐBAC+ÐBH1C=ÐBAC+ÐBHC+ÐBAC+ÐC1HB1=180°, т. е. точка H1 принадлежит окружности b(O,r). Аналогично, рассматривая SAB и SAC, получим, что точки H2 и H3 принадлежат окружности b(O,r).

ЗАДАЧА 6.

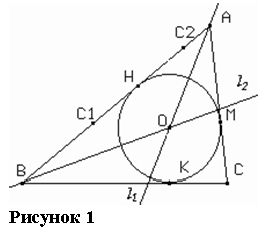
Точки C1 и С2 являются образами вершины С треугольника ABC при симметрии относительно прямых. Содержащих биссектрисы углов BAC и ABC (рис.6).Доказать, что середина отрезка C1C2 есть точка касания вписанной в треугольник окружности и сторон AB.

Решение.

Пусть i1 и i2 – прямые, содержащие биссектрисы углов BAC и ABC, а H, K, M – точки касания вписанной окружности b(O,r) со сторонами AB, BC, AC. Рассмотрим осевую симметрию относительно прямой i1. Si1 : AC®AB, C®C1. Следовательно, C1ÎAB. Так как OÎi1, то i1 – ось симметрии окружности b. Тогда Si1: M®H. Так как Si1 : C®C1, M®H, то Si1 : CM®C1H. Следовательно, CM = C1H.

 Аналогично, рассматривая осевую симметрию относительно прямой i2, получим CK = C2H. По свойству касательных, проведенных из внешней точки C к окружности b, имеем CM=CK. Тогда C1H=C2H, причем точки C1, C2, H принадлежат прямой AB. Следовательно, H – середина отрезка С1С2.

ЗАДАЧА 7.

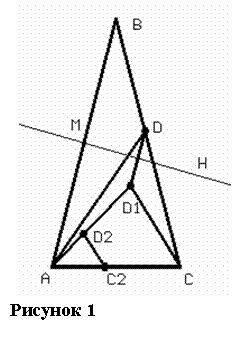
Дан равнобедренный треугольник ABC, в котором AB = BC, Ð ABC = 30°. На стороне BC взята точка D так, что бы AC: BD =  : 1. Найти угол DAC (рис.7).

Решение.

Рассмотрим осевую симметрию относительно серединного перпендикуляра MH к стороне AB. SMH:B®A, D®D1, M®M. Значит SMH:BD®AD1, ÐMBD®ÐMAD1. Следовательно, BD=AD1, DD1||AB, ÐMAD1=ÐMBD=30°. Так как ÐBAC=ÐBCA=75°, то ÐD1AC=45°. По условию AC:BD=:1. Тогда AC:AD1=:1. На прямых AC и AD1 построим точки C2 и D2 такие, что AC2=, AD2=1. Тогда в треугольнике AC2D2 имеем

D2C22=AC22+AD22–2AC2×AD2Cos45° =1.

Отсюда D2C2=1, т. е. треугольник AD2C2 является равнобедренным, а это значит, что ÐAC2D2=45°, ÐAD2C2=90°. Так как треугольники ACD1 и AC2D2 подобны, (ÐD1AC – общий, AC:AD1=AC2:AD2=:1), то ÐACD1=45°, ÐAD1C=90°. Так как DD1||AB, ÐD1DC=ÐABC=30°, то ÐDCD1=ÐBCA- ÐD1CA=75°-45°=30°. Следовательно, в равнобедренном треугольнике CD1D ÐCD1D = 120°. Тогда ÐAD1D=360° - (90° +120°) = 150°. Так как AD1=D1C=DD1, то в равнобедренном треугольнике AD1D

ÐD1AD=(180°-150°):2=15°.

Получим ÐDAC=ÐD1AC+ÐD1AD=45°+15°=60°.

Рекомендуем скачать другие рефераты по теме: курсовые, реферат на тему ресурсы.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки