Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

3. Решить уравнение: x2-2x+1=0

Рисунок 3.

Если аккуратно начертить параболу у=х2 и прямую у=2х-1, то увидим, что они имеют одну общую точку(прямая касается параболы, см. рисунок 3), х=1, у=1;уравнение имеет один корень х=1(обязательно проверить это вычислением).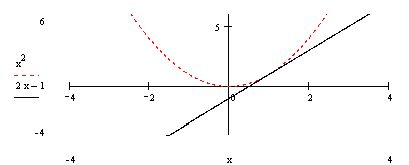
        

  II) Системы уравнений.

Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство. Графики уравнений с двумя переменными весьма разнообразны. Например, графиком уравнения 2х+3у=15 является прямая, уравнения у=0.5х2 –2 –парабола, уравнения х2 +у2=4 – окружность, и т.д..

Степень целого уравнения с двумя переменными определяется так же, как и степень целого уравнения с одной переменной. Если левая часть уравнения с двумя переменными представляет собой многочлен стандартного вида, а правая число 0, то степень уравнения считают равной степени многочлена. Для того чтобы выяснить, какова степень какого-либо уравнения с двумя переменными, его заменяют равносильным уравнением, левая часть которого – многочлен стандартного вида, а правая- нуль. Рассмотрим графический способ решения.

    Пример1:решить систему ⌠ x2 +y2 =25    (1)

                                                ⌠y=-x2+2x+5  (2)   

Построим в одной системе координат графики уравнений(Рисунок4):

Построим в одной системе координат графи)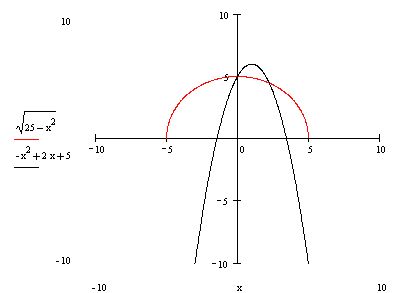

                            х2 +у2=25  и у=-х2+2х+5    

Координаты любой точки построенной окружности являются решением уравнения 1, а координаты любой точки параболы являются решением уравнения 2. Значит, координаты каждой из точек пересечения окружности и параболы удовлетворяют как первому уравнению системы, так и второму, т.е. являются решением рассматриваемой системы. Используя рисунок, находим приближённые значения координат точек пересечения графиков: А(-2,2; -4,5),   В(0;5), С(2,2;4,5), D(4;-3).Следовательно, система уравнений имеет четыре решения:

                х1≈-2,2 , у1≈-4,5;                   х2≈0,  у2≈5;

                х3≈2,2 ,  у3≈4,5;                     х4≈4,  у4≈-3.

Подставив найденные значения в уравнения системы, можно убедиться, что второе и четвёртое из этих решений являются точными, а первое и третье – приближёнными.

 III)Тригонометрические уравнения:

Тригонометрические уравнения решают как аналитически, так и графически. Рассмотрим графический способ решения на примере.

Рисунок5.

Пример1:sinx+cosx=1. Построим графики функций y=sinx u  y=1-cosx.(рисунок 5)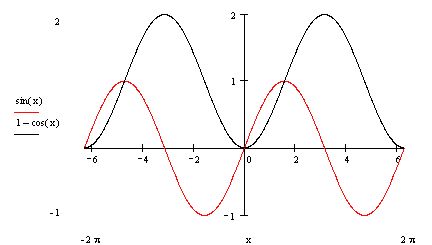
Из графика видно, что уравнение имеет 2 решения: х=2πп,где пЄZ и х=π/2+2πk,где kЄZ(Обязательно проверить это вычислениями).   Рисунок 6.

Пример2:Решить уравнение:tg2x+tgx=0. Решать это уравнение будем по принципу решения предыдущего. Сначала построим графики(См. рисунок 6)функций: y=tg2x u y=-tgx. По графику видно что уравнение имеет  2 решения: х=πп, пЄZ u x=2πk/3, где kЄZ.(Проверить это вычислениями)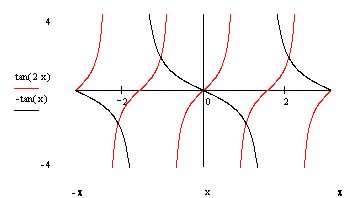
 

         

                   Применение графиков в решении неравенств.

1)Неравенства с модулем.

Пример1.

Решить неравенство |x-1|+|x+1|<4.

Рекомендуем скачать другие рефераты по теме: сочинение на тему онегин, решебник по русскому.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки